The characteristic distance at which quantum gravitational effect are significant the planck length can be determined form a suitable combination of the fundamental physical constant G h and c which of the followng correctly gives the planck length ?
To determine the Planck length Lp using the fundamental physical constants G (gravitational constant), h (Planck constant), and c (speed of light), we need to find a suitable combination of these constants that results in a length dimension.
1. Identify the Dimensions of Constants:
- The gravitational constant G has the dimensions:
(G)=(F)(m)2=(M)(L)(T−2)(M)2=(M−1L3T−2)
- The Planck constant h has the dimensions:
(h)=(E)(T)=(ML2T−2)(T)=(ML2T−1)
- The speed of light c has the dimensions:
(c)=(L)(T)=(LT−1)
2. Set Up the Dimensional Equation:
- We want to express the Planck length Lp in terms of G, h, and c:
Lp∝Gahbcc
- The dimensions of Lp are:
(Lp)=(L)
3. Write the Dimensional Equation:
- Substituting the dimensions into the equation:
(L)=(M−1L3T−2)a(ML2T−1)b(LT−1)c
- Expanding this gives:
(L)=(M−a+bL3a+2b+cT−2a−b−c)
4. Set Up the System of Equations:
- From the dimensional analysis, we can equate the powers of M, L, and T:
- For mass M:
−a+b=0(1)
- For length L:
3a+2b+c=1(2)
- For time T:
−2a−b−c=0(3)
5. Solve the System of Equations:
- From equation (1), we have b=a.
- Substitute b=a into equations (2) and (3):
- Equation (2):
3a+2a+c=1⟹5a+c=1(4)
- Equation (3):
−2a−a−c=0⟹−3a−c=0⟹c=−3a(5)
- Substitute equation (5) into equation (4):
5a−3a=1⟹2a=1⟹a=12
- Then from equation (1), b=a=12 and from equation (5):
c=−3(12)=−32
6. Final Expression for Planck Length:
- Substitute a, b, and c back into the expression for Lp:
Lp=√Ghc3
Conclusion:
The correct expression for the Planck length Lp is:
Lp=√Ghc3
- The gravitational constant G has the dimensions:
(G)=(F)(m)2=(M)(L)(T−2)(M)2=(M−1L3T−2)
- The Planck constant h has the dimensions:
(h)=(E)(T)=(ML2T−2)(T)=(ML2T−1)
- The speed of light c has the dimensions:
(c)=(L)(T)=(LT−1)
- We want to express the Planck length Lp in terms of G, h, and c:
Lp∝Gahbcc
- The dimensions of Lp are:
(Lp)=(L)
- Substituting the dimensions into the equation:
(L)=(M−1L3T−2)a(ML2T−1)b(LT−1)c
- Expanding this gives:
(L)=(M−a+bL3a+2b+cT−2a−b−c)
- From the dimensional analysis, we can equate the powers of M, L, and T:
- For mass M:
−a+b=0(1)
- For length L:
3a+2b+c=1(2)
- For time T:
−2a−b−c=0(3)
- From equation (1), we have b=a.
- Substitute b=a into equations (2) and (3):
- Equation (2):
3a+2a+c=1⟹5a+c=1(4)
- Equation (3):
−2a−a−c=0⟹−3a−c=0⟹c=−3a(5)
- Substitute equation (5) into equation (4):
5a−3a=1⟹2a=1⟹a=12
- Then from equation (1), b=a=12 and from equation (5):
c=−3(12)=−32
- Substitute a, b, and c back into the expression for Lp:
Lp=√Ghc3
The correct expression for the Planck length Lp is:
Lp=√Ghc3
Topper's Solved these Questions
Similar Questions
Planck 's constant (h) speed of length in vaccum (C) and newton 's gravitational constant (G) are three fundamental constant .Which of the following combinations of these has the dimension of length?
View SolutionA conductor is made of an isotropic material and has shape of a truncated cone. A battery of constant emf is connected across it and its left end is earthed as shown. If at a certain section at a distance x form left end, electric field intensity and the rate of generation of heat per unit length are E and H respectively, which of the following graphs is (are) correct?
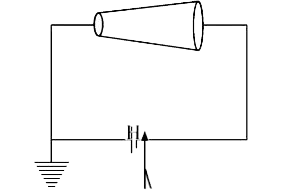
View Solution
Knowledge Check
If velocity of light c, planck's constant h and gravitational constnat G are taken as fundamental quantities then the dimensions of the length will be
A√chGB√hGc5C√hGc3D√hc3G
Experiment shows that two perfectly neutral parallel metal plates separated by a small distance d sttract eachother via a very weak force, known as the Casimir force. The force per unit area of the plates, F, depends only on the Planck constant h, on the speed of light c, and on d. Which of the following has the best chance of being correct for F?
View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration

A. the normal reaction on the bead will be constant h magnitude and direction both
B. the magnitude of the normal reaction on the bead will be variable
C. the magnitude of friction force on the bead will be constant
D. the magnitude of friction force on the bead will be variable
View SolutionA flywheel can rotate in order to store kinetic energy. The flywheel is a uniform disc made of a material with a density ρ and tensile strength σ (measured in Pascals), a radiys r, and a thickness h. The flywheel is rotating at the maximum possible angular velocity so that it does not break. Which of the following expression correctly gives the maximum kinetic energy kilogram that can be stored in the flywheel? Assume that α is a dimensionless constant.
View SolutionIf velocity of light c, Planck's constant h ,Gravitational constant G are taken as fundamental quantites, then express mass, length and time in terms of dimensions of these quantites.
View SolutionIf C the velocity of light, h planck's constant and G Gravitational constant are taken as fundamental quantities, then the dimensional formula of mass is
View SolutionExpression for time in terms of G (universal gravitational constant), h (Planck constant) and c (speed of light) is proportional to:
View SolutionA large number of pendulums with identical bobs (mass m) but varying lengths are suspended from a thick thread. Another pendulum of a heavier bob (mass M) is also suspended from the same thred as shown.

This pendulum with the heavier bob is used as a 'driver' to drive the other pendulums called as 'driven' pendulums. Assume that the amplitude of the driver is maintained constant (by some suitable mechanism). Let the frequency of the driver be f0
Which of the following will give a straight line graph ?
View Solution
