A thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and z' axes will be :
1:5
1:3
1:4
1:2
The correct Answer is:B
To find the ratio of the moment of inertia of a thin circular disk about the z-axis and the z' axis, we can follow these steps:
Step 1: Moment of Inertia about the z-axis
The moment of inertia (I_z) of a thin circular disk about its central axis (z-axis) is given by the formula:
Iz=12mr2
where m is the mass of the disk and r is the radius of the disk.
Step 2: Moment of Inertia about the z' axis
To find the moment of inertia about the z' axis (which is parallel to the z-axis and located at a distance r from it), we can use the parallel axis theorem. The parallel axis theorem states that:
Iz′=Iz+md2
where d is the distance between the two axes. In this case, d=r.
Substituting the values, we get:
Iz′=12mr2+mr2
Iz′=12mr2+22mr2=32mr2
Step 3: Ratio of Moments of Inertia
Now, we can find the ratio of the moment of inertia about the z-axis to that about the z' axis:
Ratio=IzIz′=12mr232mr2
The mr2 terms cancel out:
Ratio=1/23/2=13
Conclusion
Thus, the ratio of the moment of inertia about the z-axis to that about the z' axis is:
Ratio=1:3
The moment of inertia (I_z) of a thin circular disk about its central axis (z-axis) is given by the formula:
Iz=12mr2
where m is the mass of the disk and r is the radius of the disk.
To find the moment of inertia about the z' axis (which is parallel to the z-axis and located at a distance r from it), we can use the parallel axis theorem. The parallel axis theorem states that:
Iz′=Iz+md2
where d is the distance between the two axes. In this case, d=r.
Iz′=12mr2+mr2
Iz′=12mr2+22mr2=32mr2
Now, we can find the ratio of the moment of inertia about the z-axis to that about the z' axis:
Ratio=IzIz′=12mr232mr2
The mr2 terms cancel out:
Ratio=1/23/2=13
Thus, the ratio of the moment of inertia about the z-axis to that about the z' axis is:
Ratio=1:3
Topper's Solved these Questions
Similar Questions
A planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
View SolutionFour identical rods, each of mass m and length l, make a square frame in the xy plane as shown in Fig.
a. Calculate its moment of inertia about the x-and y-axes.
b. Also, calculate its moment of inertia about the z-axis.

View Solution
Knowledge Check
A thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 Aml2BzeroCml2π2Dml22π2
Aml2BzeroCml2π2Dml22π2
A uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The ratio of moment of inertia of the loop about x-axis to that about y-axis is

View SolutionA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be

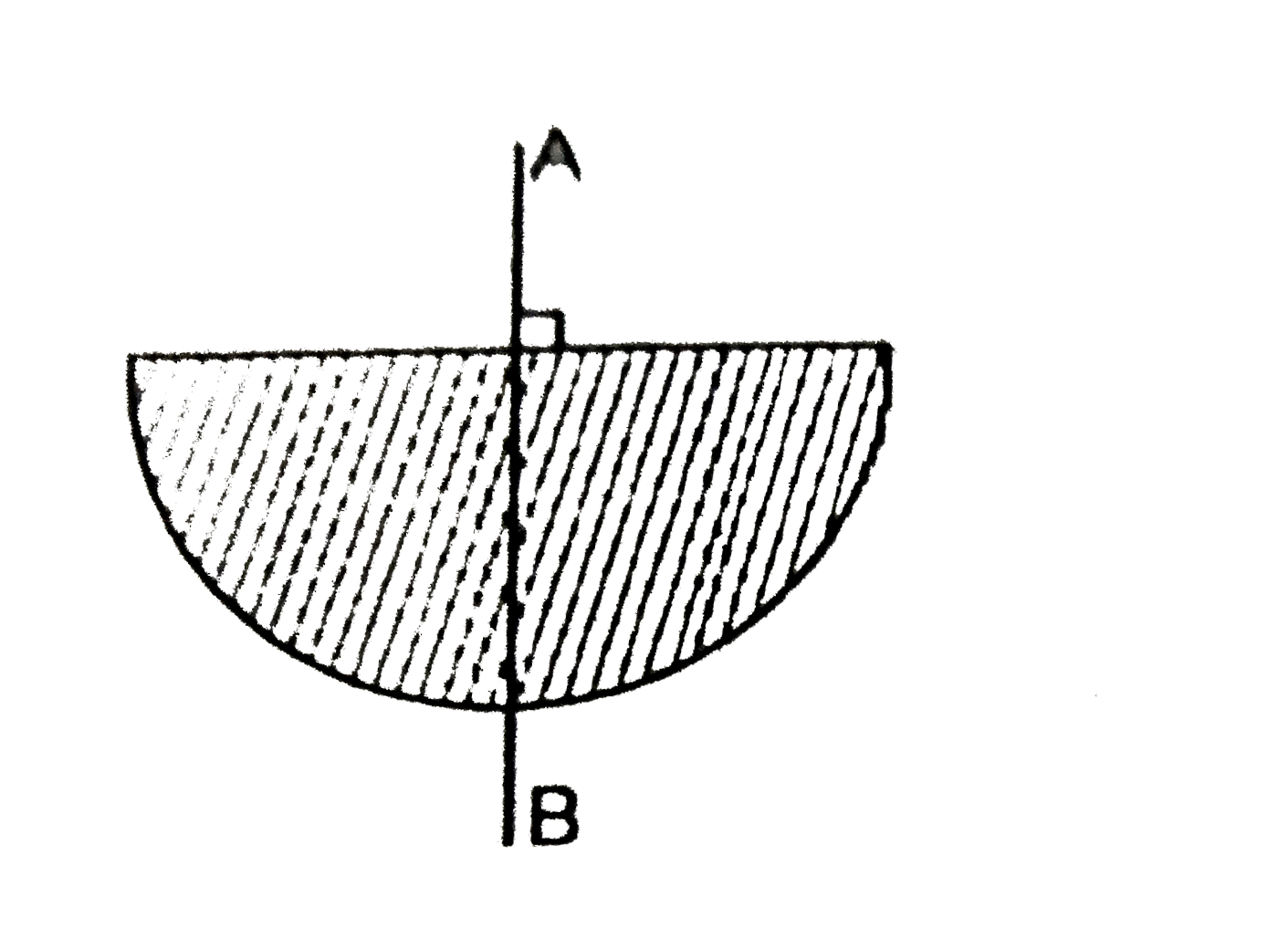
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
View SolutionOne circular ring and one circular disc, both are having the same mass and radius. The ratio of their moments of inertia about the axes passing through their centres and perpendicular to their planes, will be
View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be

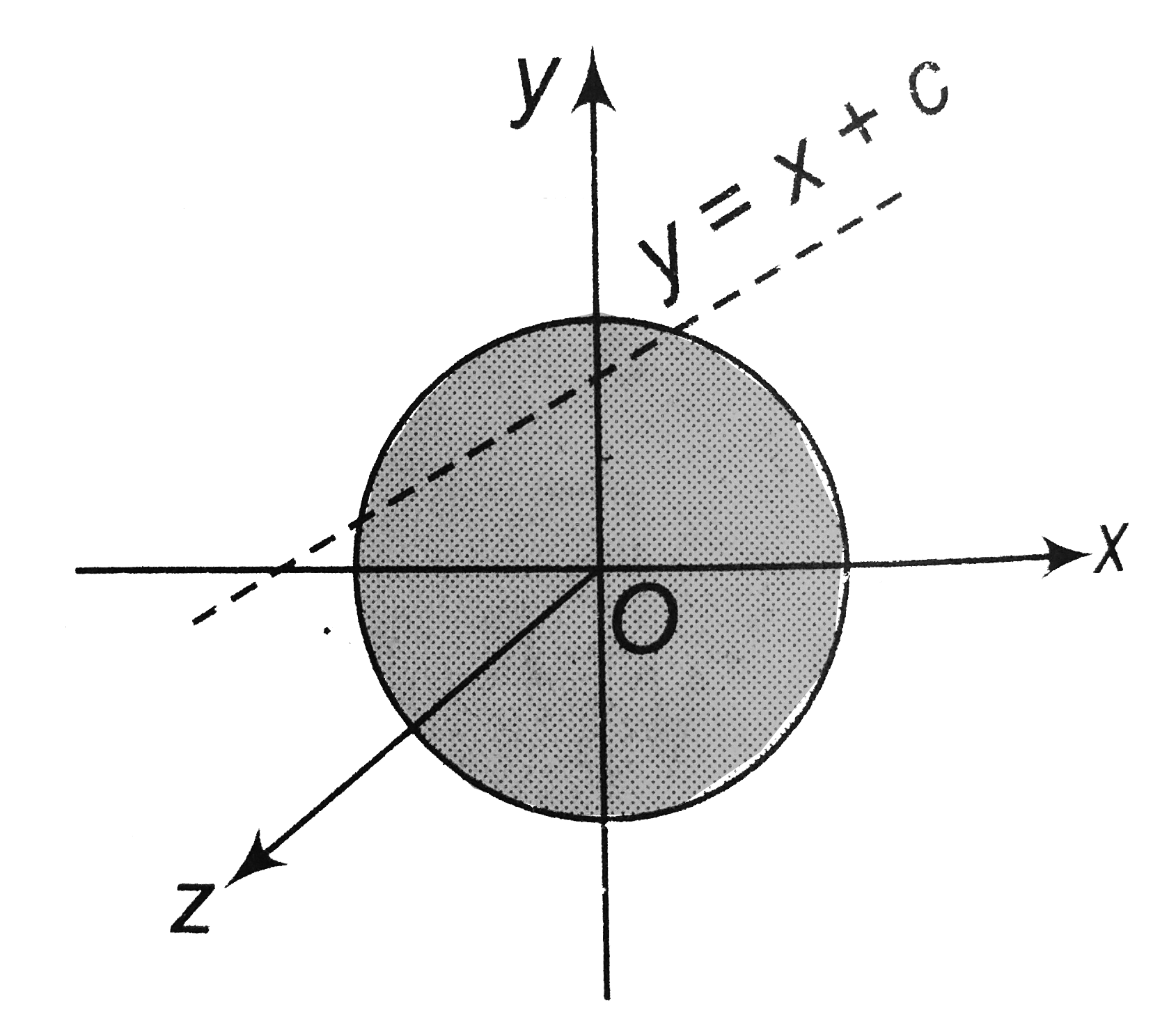
View SolutionA uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
 .
.
View SolutionMoment of inertia of a ring about its diameteric axis is I. Two such rings are welded as shown in figure. The new moment of inertia about XX' axis is
_PHY_E05_247_Q01.png)
View Solution
