Two identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameters, and the force between them is F. A third identical conducting spheres, C,is uncharged. Sphere C is first touched to A, then to B, and then removed. As a result, the force between A and B would be equal to :
F
3F8
3F4
F2
The correct Answer is:B
To solve the problem step by step, we will analyze the situation involving the three identical conducting spheres A, B, and C.
Step 1: Initial Charges on Spheres A and B
Let the charge on sphere A be Q and the charge on sphere B also be Q. The force F between them can be expressed using Coulomb's law:
F=kQ2R2
where k is Coulomb's constant and R is the distance between the centers of the spheres.
Hint for Step 1: Remember that the force between two charges is given by Coulomb's law.
Step 2: Touching Sphere C to Sphere A
Sphere C is initially uncharged. When it touches sphere A, the total charge Q on sphere A is shared equally between A and C. After touching:
- Charge on A becomes Q2
- Charge on C becomes Q2
Hint for Step 2: When two identical conductors touch, the charge distributes equally between them.
Step 3: Touching Sphere C to Sphere B
Next, sphere C (which now has a charge of Q2) is brought into contact with sphere B. The total charge on sphere B before contact is Q. When they touch, the total charge Q+Q2=3Q2 is shared equally:
- Charge on B becomes 3Q4
- Charge on C becomes 3Q4
Hint for Step 3: Again, remember that the charge distributes equally between two identical conductors when they touch.
Step 4: Final Charges on Spheres A and B
After the two contacts, the charges on the spheres are:
- Charge on A: Q2
- Charge on B: 3Q4
Hint for Step 4: Keep track of the charges after each contact to ensure accuracy.
Step 5: Calculating the New Force Between A and B
Now, we can calculate the new force F′ between spheres A and B using the new charges:
F′=k(Q2)(3Q4)R2=k3Q28R2
Step 6: Relating the New Force to the Original Force
From the original force F=kQ2R2, we can express the new force in terms of the original force:
F′=38F
Conclusion
Thus, the new force between spheres A and B after the interactions with sphere C is:
F′=38F
Final Answer: The force between A and B would be equal to 38F.
Let the charge on sphere A be Q and the charge on sphere B also be Q. The force F between them can be expressed using Coulomb's law:
F=kQ2R2
where k is Coulomb's constant and R is the distance between the centers of the spheres.
Sphere C is initially uncharged. When it touches sphere A, the total charge Q on sphere A is shared equally between A and C. After touching:
- Charge on A becomes Q2
- Charge on C becomes Q2
Next, sphere C (which now has a charge of Q2) is brought into contact with sphere B. The total charge on sphere B before contact is Q. When they touch, the total charge Q+Q2=3Q2 is shared equally:
- Charge on B becomes 3Q4
- Charge on C becomes 3Q4
After the two contacts, the charges on the spheres are:
- Charge on A: Q2
- Charge on B: 3Q4
Now, we can calculate the new force F′ between spheres A and B using the new charges:
F′=k(Q2)(3Q4)R2=k3Q28R2
From the original force F=kQ2R2, we can express the new force in terms of the original force:
F′=38F
Thus, the new force between spheres A and B after the interactions with sphere C is:
F′=38F
Topper's Solved these Questions
Similar Questions
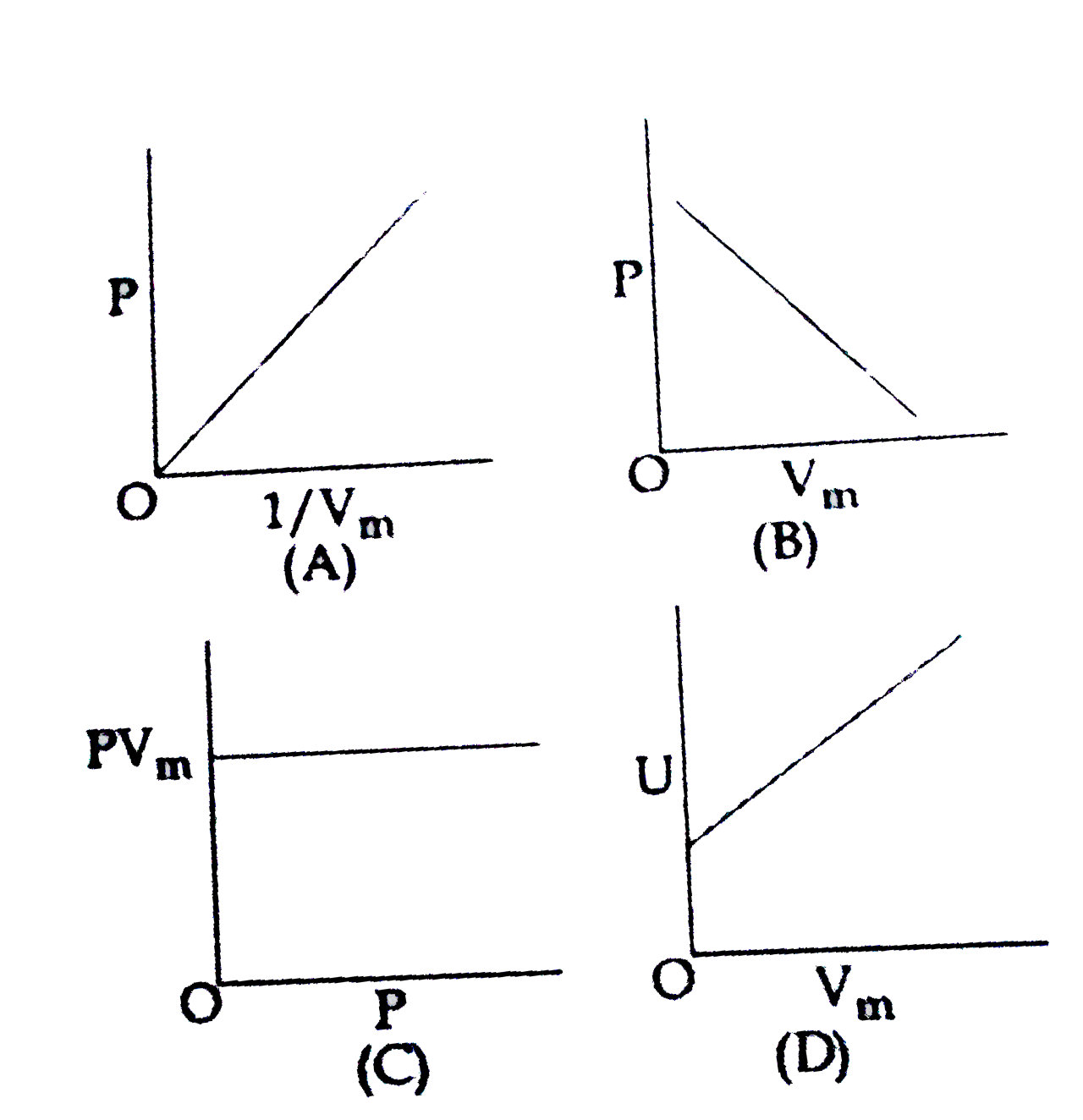
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionTwo identical conducting spheres 1 and 2 carry equal amounts of charge and are ficed apart at a certain distance larger than their diameters. The spheres repel each other with an electrical force of 88mN. A thired identical sphere 3, having an insulating handle and initially uncharged, is touched first to sphere 1 and then to sphere 2 and finally removed. Find the force between spheres 1 and 2 as shown if Figure.
 ,
,
View SolutionTwo equally charged, indentical metal spheres A and B repel each other with a force F" . The spheres are kept fixed with a distance r between them. A third identical, but uncharged sphere C is brought in contact with A and The magnitude of the net electric force on C is
View SolutionConsider three identical metal spheres A,B and C. Spheres A carres charge +6q carries no charge . Spheres A and B are touchd together and them separated. Sphere C is then touched to sphere A and separated from it . Finally the sphere C is touched to sphere B and separated from it . Find the final chage on the sphere C.
View SolutionTwo identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameters, and the force between them is F. A third identical conducting spheres, C,is uncharged. Sphere C is first touched to A, then to B, and then removed. As a result, the force between A and B would be equal to :
View SolutionThere are two charged identical metal spheres A and B repel each other with a force 3×10−5N. Another identical uncharged sphere C is touched with A and then placed at the mid-point between A and B. Net force on C is
View SolutionIn Frame 1, two identical conducting spheres, A and B, carry equal amounts of excess charge that have the same sign. The spheres are separated by a distance d, and sphere A exerts an electrostatic force on sphere B that has a magnitude F. A third sphere, C, Which is handled only by an insulating rod, is introduced in Frame 2. Sphere C is identical to A and B except that it initially uncharged. Sphere C is touched first to sphere A, in Frame 2, and then to sphere B, in Frame 3, and is finally removed in Frame 4.
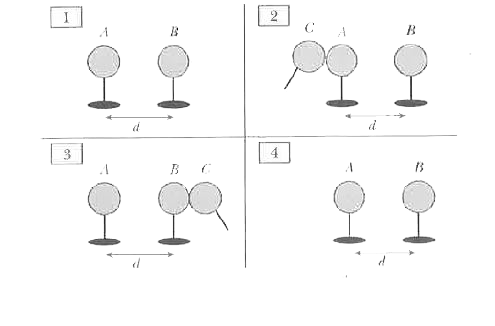
Determine the magnitude of the electrostatic force that sphere A exerts on sphere B in Frame 4.
View SolutionTwo identical metallic sphere's A and B having charges +4Qand−10Q are kept a certain distance apart. A third identical uncharged sphere C is first placed in contact with sphere A and then with sphere B. Spheres A and B are then brought in contact and then separated. Find the charges on the spheres A and B.
View SolutionCharges on identical spheres A and B are equal. When the separation between them is 1 m, the repulsion between them is 80 N. Now, another identical and uncharged sphere C is brought in contact with A and then separated. Then, C is brought in contact with B and then separated. What will be the new force between A and B ?
View SolutionA and B are two identical point sized metal spheres each holding the same charge .q.. These two are separated by certain distance and the mutual electrostatic force between them is F. If a third identical uncharged sphere .C. is touched with A and kept exactly at the midpoint of line joining A and B, what is the resulting force on C and its direction?
View SolutionTwo equally charged, identical metal spheres A and B rpepel each other with a force F. the spheres are kept fixed with a distance r between them. A third identical, but uncharged sphere C is brought in contact with A and then placed at the mid-point of thr line joining A and B. the magnitude of the net electric force on C is
View SolutionA and B are two identical point sized metal spheres each holding the same charge q . These two are separated by certain distance and the mutual electrostatic force between them is F. if a third identical uncharged sphere 'C' is touched with A and kept exactly at the midpoint of line joining A and B, what is the resulting force on C and its direction ?
View SolutionTwo equally charged, indentical metal spheres A and B repel each other with a force F" . The spheres are kept fixed with a distance r between them. A third identical, but uncharged sphere C is brought in contact with A and removed. The magnitude of the net electric force on A is
View Solution
