One mole of and ideal monoatomic gas is compressed isothermally in a rigid vessel to double its pressure at room temperature, 27∘C . The work done on the gas will be :
300 R ln 7
300 R ln 2
300 R
300 R ln 6
The correct Answer is:B
To solve the problem of calculating the work done on one mole of an ideal monoatomic gas compressed isothermally in a rigid vessel to double its pressure at room temperature (27°C), we can follow these steps:
1. Understanding the Isothermal Process:
In an isothermal process, the temperature remains constant. For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) is given by the ideal gas law:
PV=nRT
where n is the number of moles, R is the universal gas constant, and T is the absolute temperature in Kelvin.
2. Convert Temperature to Kelvin:
The given temperature is 27°C. To convert this to Kelvin:
T=27+273=300K
3. Initial and Final Pressures:
Let the initial pressure be P1 and the final pressure be P2. According to the problem, the pressure is doubled:
P2=2P1
4. Work Done in Isothermal Process:
The work done on the gas during an isothermal process can be calculated using the formula:
W=−nRTln(V2V1)
Since the volume is constant in a rigid vessel, we can relate the volumes to pressures using the ideal gas law:
V2V1=P1P2
Substituting P2=2P1:
V2V1=P12P1=12
5. Substituting into Work Formula:
Now we can substitute this back into the work done formula:
W=−nRTln(12)
Since n=1 mole and R is the universal gas constant, we have:
W=−RTln(12)
6. Calculate Work Done:
Now substituting the values:
W=−R⋅300⋅ln(12)
Using the property of logarithms, ln(12)=−ln(2):
W=300Rln(2)
7. Final Result:
Therefore, the work done on the gas is:
W=300Rln(2)
Final Answer:
The work done on the gas will be 300Rln(2).
---
In an isothermal process, the temperature remains constant. For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) is given by the ideal gas law:
PV=nRT
where n is the number of moles, R is the universal gas constant, and T is the absolute temperature in Kelvin.
The given temperature is 27°C. To convert this to Kelvin:
T=27+273=300K
Let the initial pressure be P1 and the final pressure be P2. According to the problem, the pressure is doubled:
P2=2P1
The work done on the gas during an isothermal process can be calculated using the formula:
W=−nRTln(V2V1)
Since the volume is constant in a rigid vessel, we can relate the volumes to pressures using the ideal gas law:
V2V1=P1P2
Substituting P2=2P1:
V2V1=P12P1=12
Now we can substitute this back into the work done formula:
W=−nRTln(12)
Since n=1 mole and R is the universal gas constant, we have:
W=−RTln(12)
Now substituting the values:
W=−R⋅300⋅ln(12)
Using the property of logarithms, ln(12)=−ln(2):
W=300Rln(2)
Therefore, the work done on the gas is:
W=300Rln(2)
The work done on the gas will be 300Rln(2).
Topper's Solved these Questions
Similar Questions
When an ideal gas is compressed isothermally then its pressure increase because:
View SolutionOne mole of a gas is heated at constant pressure to raise its temperature by 1∘C. The work done in joules is
View SolutionIf one mole of gas doubles its volume at temperature T isothermally then work done by the gas is
View SolutionAt 27∘C, one mole of an ideal gas is compressed isothermally and reversibly from a pressure of 2 atm to 10 atm. Calculate ΔU and q.
View SolutionOne mole of an ideal and monoatomic gas is expanded reversibly and isothermally at 298K temperature according to the given diagram, calculate work done.
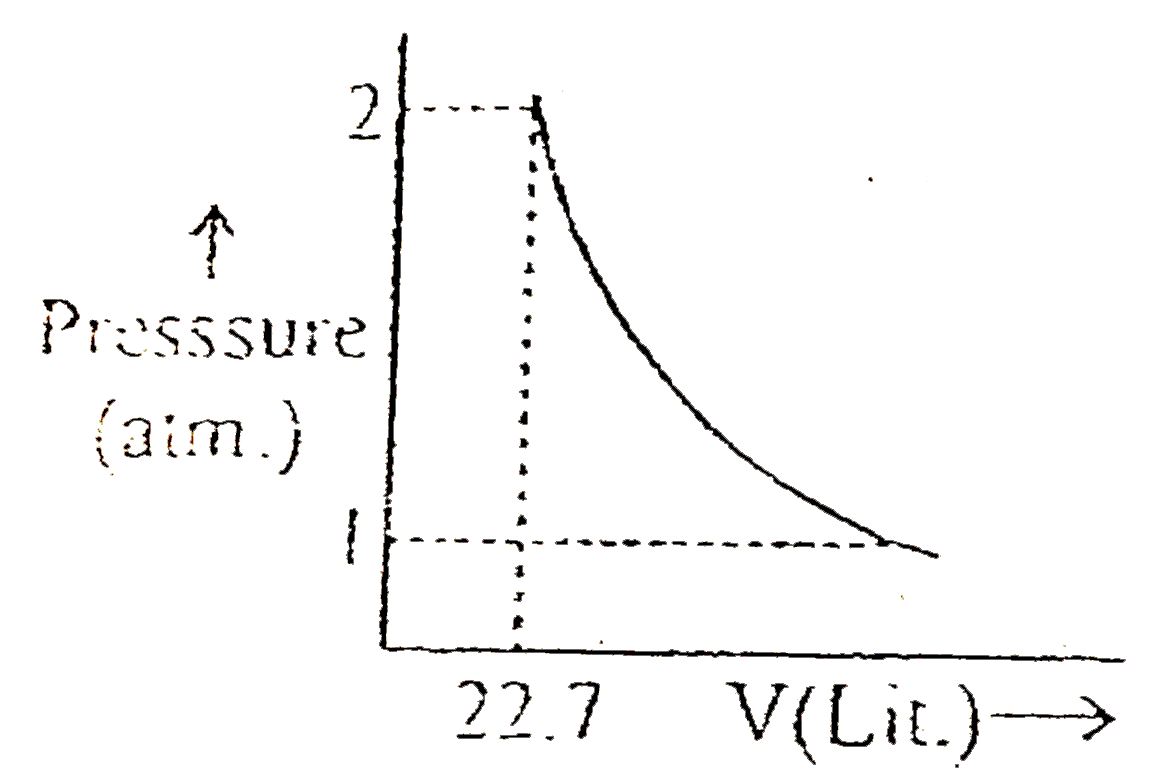
View SolutionAn ideal gas at 300K is expanded isothermally to double its volume,then pressure of the gas will be
View SolutionOne gm mol of a diatomic gas (γ=1.4) is compressed adiabatically so that its temperature rises from 27∘C to 127∘C . The work done will be
View SolutionOne gm mol of a diatomic gas (γ=1.4) is compressed adiabatically so that its temperature rises from 27∘C to 127∘C . The work done will be
View SolutionTwo moles of an ideal monatomic gas is heated at constant pressure so that its temperature increases from 127∘C to 227∘C , then work done by gas
View SolutionA monoatomic gas is compressed adiabatically to 8/27 of its initial volume, if initial temperature is 27∘C, then increase in temperature
View Solution
