The dimension of magnetic field in M, L, T and C (Coulomb) is given as :
MLT−1C−1
MT−2C−2
MT−1C−1
MT−2C−1
The correct Answer is:C
To find the dimensions of the magnetic field B in terms of mass M, length L, time T, and charge C, we can start by using the formula for the magnetic force acting on a current-carrying wire.
1. Understanding the Magnetic Force:
The magnetic force F on a current-carrying wire of length L in a magnetic field B is given by the equation:
F=BILsin(θ)
For simplicity, we can consider the case where the wire is perpendicular to the magnetic field, so sin(θ)=1. Thus, we have:
F=BIL
2. Rearranging the Formula:
We can rearrange the formula to express the magnetic field B:
B=FIL
3. Finding Dimensions of Each Quantity:
- The dimension of force F is given by:
(F)=(M)(L)(T−2)=MLT−2
- The dimension of current I is represented as charge per unit time:
(I)=(Q)(T)=CT−1
- The dimension of length L is simply:
(L)=L
4. Substituting Dimensions into the Formula:
Now we can substitute the dimensions of force, current, and length into the equation for B:
(B)=(F)(I)(L)=MLT−2(CT−1)(L)
5. Simplifying the Expression:
When we simplify this expression, we get:
(B)=MLT−2CTL=MCT−1
6. Final Result:
Therefore, the dimensions of the magnetic field B can be expressed as:
(B)=ML−1T−2C−1
Conclusion:
The dimensions of the magnetic field B in terms of mass M, length L, time T, and charge C are:
(B)=ML−1T−2C−1
The magnetic force F on a current-carrying wire of length L in a magnetic field B is given by the equation:
F=BILsin(θ)
For simplicity, we can consider the case where the wire is perpendicular to the magnetic field, so sin(θ)=1. Thus, we have:
F=BIL
We can rearrange the formula to express the magnetic field B:
B=FIL
- The dimension of force F is given by:
(F)=(M)(L)(T−2)=MLT−2
- The dimension of current I is represented as charge per unit time:
(I)=(Q)(T)=CT−1
- The dimension of length L is simply:
(L)=L
Now we can substitute the dimensions of force, current, and length into the equation for B:
(B)=(F)(I)(L)=MLT−2(CT−1)(L)
When we simplify this expression, we get:
(B)=MLT−2CTL=MCT−1
Therefore, the dimensions of the magnetic field B can be expressed as:
(B)=ML−1T−2C−1
The dimensions of the magnetic field B in terms of mass M, length L, time T, and charge C are:
(B)=ML−1T−2C−1
Topper's Solved these Questions
Similar Questions
Dimensions of magnetic field intensity is
View SolutionThe dimensions of resistivity in terms of M, L, T and Q, where Q stands for the dimensions of charge is
View SolutionThe magnetic field in a plane electromagnetic wave is given by B=200(μT)sin4×10'−5s1(t−x/c). Find the maximum magnetic and electric fields.
View SolutionThe magnetic field in a plane electromagnetic wave is given by →B=2×10−7 [sin(0.5×103x+1.5×1011t)ˆj]. The electric field is given by (where B is in T , x is in m and t in s)
View SolutionIf discharge rate is given by V=πPr48μl then find out the dimensions of μ by taking velocity (v), time (T) and mass (M) as fundamental units.
View SolutionThe dimensions of the quantity L/C is identical to
View SolutionIf ε0,B,V represent permitivity of free space, magnitude of magnetic field and volume of space respectively, then the dimension of ε0B2V is [MaLbTc]. Find a+b+c.
View SolutionIn Fig. there is a frame consisting of two square loops having resistors and inductors as shown. This frame is placed in a uniform but time-varying magnetic field in such a way that one of the loops is placed in crossed magentic field and the other is placed in dot magnetic field. Both magnetic fields are perpendicular to the planes of the loops.
If the magnetic field is given by B=(20+10t)Wbm−2 in both regions [l=20cm,b=10cm, and R=10Ω, L=10H),
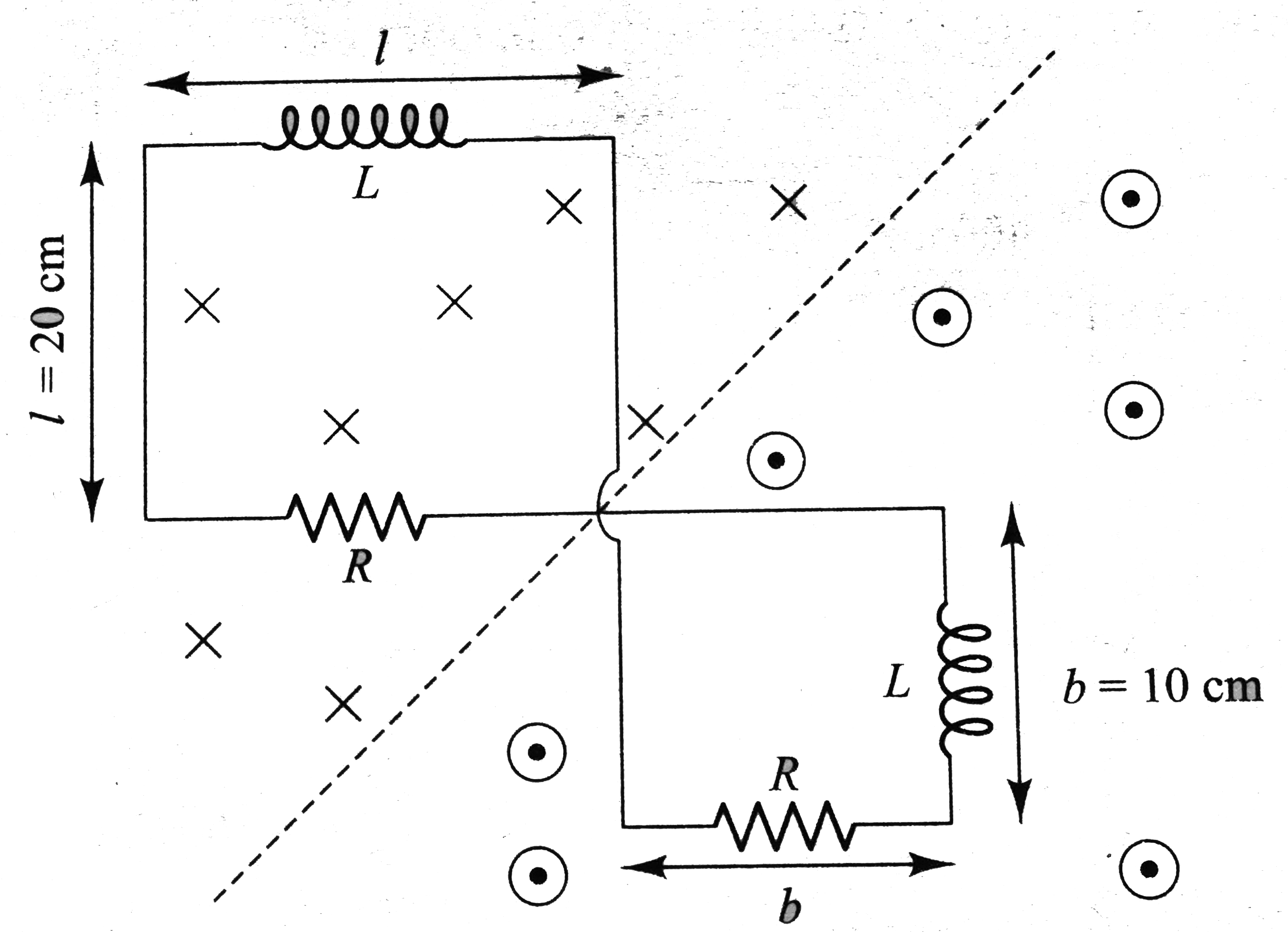
The current in the frame as a funtion of time will be
View SolutionIn Fig. there is a frame consisting of two square loops having resistors and inductors as shown. This frame is placed in a uniform but time-varying magnetic field in such a way that one of the loops is placed in crossed magentic field and the other is placed in dot magnetic field. Both magnetic fields are perpendicular to the planes of the loops.
If the magnetic field is given by B=(20+10t)Wbm−2 in both regions [l=20cm,b=10cm, and R=10Ω, L=10H),
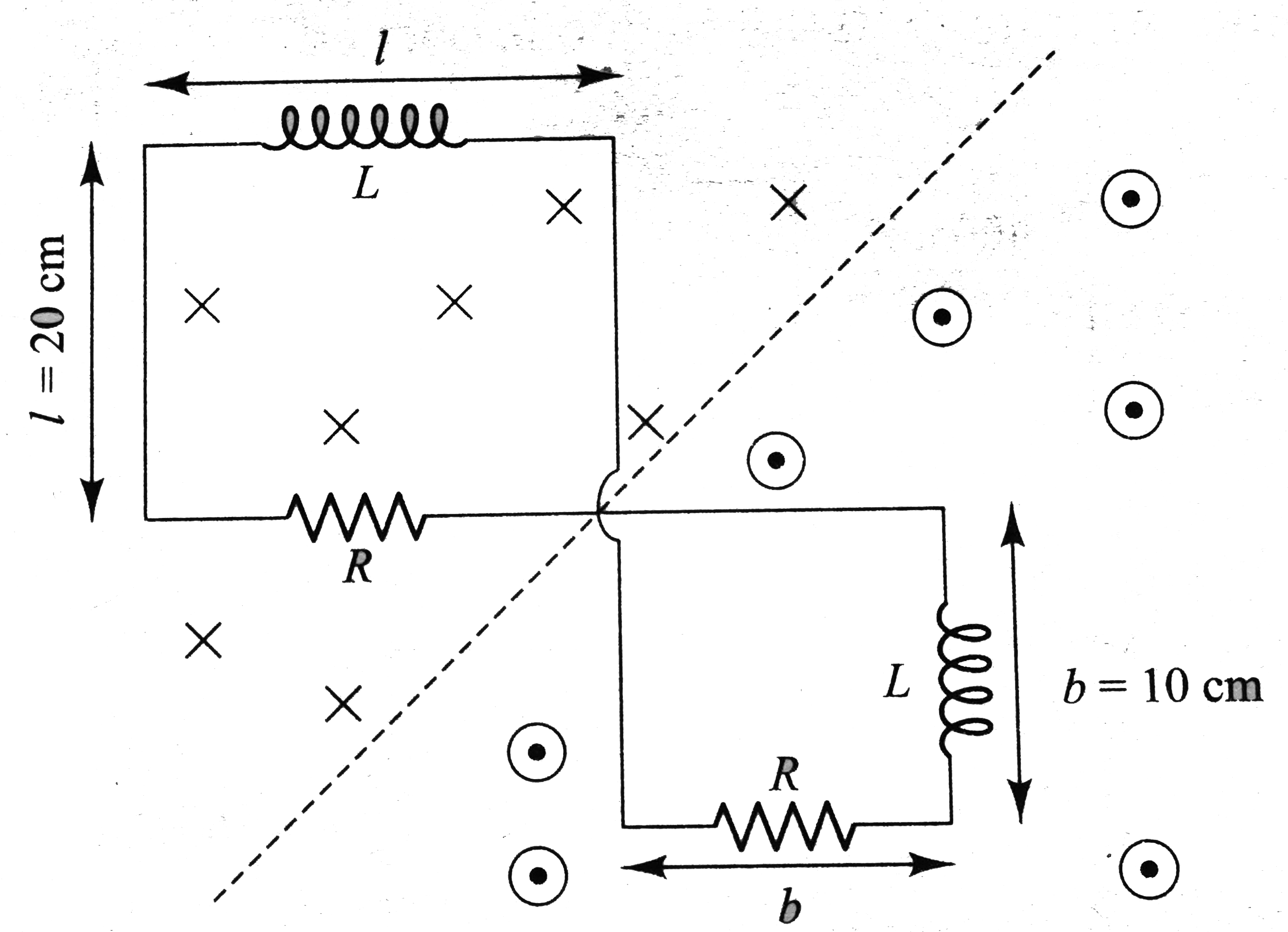
The direction in induced current in the bigger loop will be
View SolutionThe dimensional formula fo resistivity in terms of M,L,T and Q where Q stands for the dimensions of charge is
View Solution
