A block of mass 0.50kg is moving with a speed of 2.00m/s on a smooth surface. It strikes another mass of 1kg at rest and they move as a single body. The energy loss during the collision is
0.16 J
1.00 J
0.67 J
0.34 J
The correct Answer is:C
To find the energy loss during the collision between the two blocks, we can follow these steps:
Step 1: Identify the masses and initial speeds
- Mass of the first block, m1=0.50kg
- Initial speed of the first block, v1=2.00m/s
- Mass of the second block, m2=1.00kg
- Initial speed of the second block, v2=0m/s (since it is at rest)
Step 2: Calculate the initial momentum
The total initial momentum Pinitial of the system is given by:
Pinitial=m1v1+m2v2=(0.50kg×2.00m/s)+(1.00kg×0)=1.00kg m/s
Step 3: Calculate the final mass and use conservation of momentum
After the collision, the two blocks stick together and move as a single body. The combined mass mf is:
mf=m1+m2=0.50kg+1.00kg=1.50kg
Using conservation of momentum:
Pfinal=mfvf
Setting Pinitial=Pfinal:
1.00kg m/s=1.50kg×vf
Solving for vf:
vf=1.00kg m/s1.50kg=23m/s
Step 4: Calculate the initial kinetic energy
The initial kinetic energy KEinitial of the system is:
KEinitial=12m1v21+12m2v22
Substituting the values:
KEinitial=12(0.50kg)(2.00m/s)2+12(1.00kg)(0)2
Calculating:
KEinitial=12×0.50×4=1.00J
Step 5: Calculate the final kinetic energy
The final kinetic energy KEfinal after the collision is:
KEfinal=12mfv2f=12(1.50kg)(23m/s)2
Calculating:
KEfinal=12×1.50×49=1.50×418=618=13J≈0.33J
Step 6: Calculate the energy loss
The energy loss during the collision is given by:
Energy loss=KEinitial−KEfinal=1.00J−0.33J≈0.67J
Final Answer
The energy loss during the collision is approximately 0.67J.
---
- Mass of the first block, m1=0.50kg
- Initial speed of the first block, v1=2.00m/s
- Mass of the second block, m2=1.00kg
- Initial speed of the second block, v2=0m/s (since it is at rest)
The total initial momentum Pinitial of the system is given by:
Pinitial=m1v1+m2v2=(0.50kg×2.00m/s)+(1.00kg×0)=1.00kg m/s
After the collision, the two blocks stick together and move as a single body. The combined mass mf is:
mf=m1+m2=0.50kg+1.00kg=1.50kg
Using conservation of momentum:
Pfinal=mfvf
Setting Pinitial=Pfinal:
1.00kg m/s=1.50kg×vf
Solving for vf:
vf=1.00kg m/s1.50kg=23m/s
The initial kinetic energy KEinitial of the system is:
KEinitial=12m1v21+12m2v22
Substituting the values:
KEinitial=12(0.50kg)(2.00m/s)2+12(1.00kg)(0)2
Calculating:
KEinitial=12×0.50×4=1.00J
The final kinetic energy KEfinal after the collision is:
KEfinal=12mfv2f=12(1.50kg)(23m/s)2
Calculating:
KEfinal=12×1.50×49=1.50×418=618=13J≈0.33J
The energy loss during the collision is given by:
Energy loss=KEinitial−KEfinal=1.00J−0.33J≈0.67J
The energy loss during the collision is approximately 0.67J.
Topper's Solved these Questions
- JEE MAINSBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINSExercise:Chemistry
Explore 1 Video
- JEE MAINBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINExercise:All Questions
Explore 452 Videos
- JEE MAINS 2020Book:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINS 2020Exercise:PHYSICS
Explore 250 Videos
Similar Questions
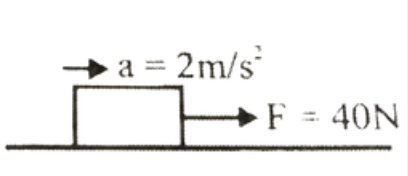
A block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
View SolutionA block of mass 1.2 kg moving at a speed of 20 cm /s collides head on with a similar block kept at rest. The coefficient of restitution is 3/5. Find the loss of kinetic energy during the collision.
View SolutionA block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
View SolutionA block of mass 2.0 kg moving at 2.0 m/s collides head on with another block of equal mass kept at rest. a. Find the maximum possible loss in kinetic energy due to the collision. b.If the actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
View SolutionA block of mass 2.00 kg moving at a speed of 10.0 m/s accelerates at 3.0 ms2 for 5.00 s. Compute its final kinetic enegy.
View SolutionA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be

View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA ball of mass 5 kg moving with speed 8 m/s collides head on with another stationary ball of mass 15 kg. If collision is perfectly inelastic, then loss in kinetic energ is
View SolutionA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View Solution
