Two coaxial solenoids are made by winding thin insulated wire over a pipe of cross-sectional area A=10cm2 and length =20cm. If one of the solenoid has 300 turns and the other 400 turns, their mutual indcutance is
2.4π×10−5H
4.8π×10−4H
4.8π×10−5H
2.4π×10−4H
The correct Answer is:D
To find the mutual inductance M of two coaxial solenoids, we can use the formula:
M=μ0n1n2Al
where:
- μ0 is the permeability of free space, approximately 4π×10−7H/m,
- n1 is the number of turns in the first solenoid,
- n2 is the number of turns in the second solenoid,
- A is the cross-sectional area of the solenoids in square meters,
- l is the length of the solenoids in meters.
1. Identify the given values:
- n1=300 turns (for the first solenoid)
- n2=400 turns (for the second solenoid)
- A=10cm2=10×10−4m2=10−3m2
- l=20cm=0.2m
2. Substitute the values into the formula:
M=(4π×10−7)×300×400×(10−3)0.2
3. Calculate the product of turns:
n1n2=300×400=120000=1.2×105
4. Substitute this back into the equation:
M=(4π×10−7)×(1.2×105)×(10−3)0.2
5. Simplify the equation:
M=4π×1.2×10−50.2
6. Calculate 1.20.2:
1.20.2=6
7. Now substitute back:
M=4π×6×10−5=24π×10−5
8. Convert to standard form:
M=2.4π×10−4H
Final Answer:
M=2.4π×10−4H
- μ0 is the permeability of free space, approximately 4π×10−7H/m,
- n1 is the number of turns in the first solenoid,
- n2 is the number of turns in the second solenoid,
- A is the cross-sectional area of the solenoids in square meters,
- l is the length of the solenoids in meters.
- n1=300 turns (for the first solenoid)
- n2=400 turns (for the second solenoid)
- A=10cm2=10×10−4m2=10−3m2
- l=20cm=0.2m
M=(4π×10−7)×300×400×(10−3)0.2
n1n2=300×400=120000=1.2×105
M=(4π×10−7)×(1.2×105)×(10−3)0.2
M=4π×1.2×10−50.2
1.20.2=6
M=4π×6×10−5=24π×10−5
M=2.4π×10−4H
M=2.4π×10−4H
Topper's Solved these Questions
Similar Questions
The number of turns, cross-sectional area and length for four solenoids are given in the following table.

The solenoid with maximum self inductance is :
View SolutionTwo toroidal solenoids are wound around the same pipe so that the magnetic field of one passes through the turns of the other. Solenoid 1 has 700 turns and solenoid 2 has 400 turns. When the current in solenoid 1 is 6.52A, the average flux through each turn of solenoid 2 is 0.0320Wb.
(a) What is the mutual inductance of the pair of solenoids?
(b) When the current in solenoid 2 is 2.54A, what is the average flux through each solenoid 1?
View Solution
Knowledge Check
The self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
A0.86mHB1.06mHC1.26mHD1.46mHA solenoid of cross-sectional area 2×10−4m2 and 900 turns has 0.6Am2 magnetic moment. Then the current flowing through it is
A2.4AB2.34mAC3.33AD3.33mA
A circular coil with a cross-sectional area of 4cm2 has 10 turns. It is placed at the center of a long solenoid that has 15 turns/cm and a cross sectional area of 10cm2, shown in the figure. The axis of the coil conicides with the axis of the solenoid. What is their mutual inductance?
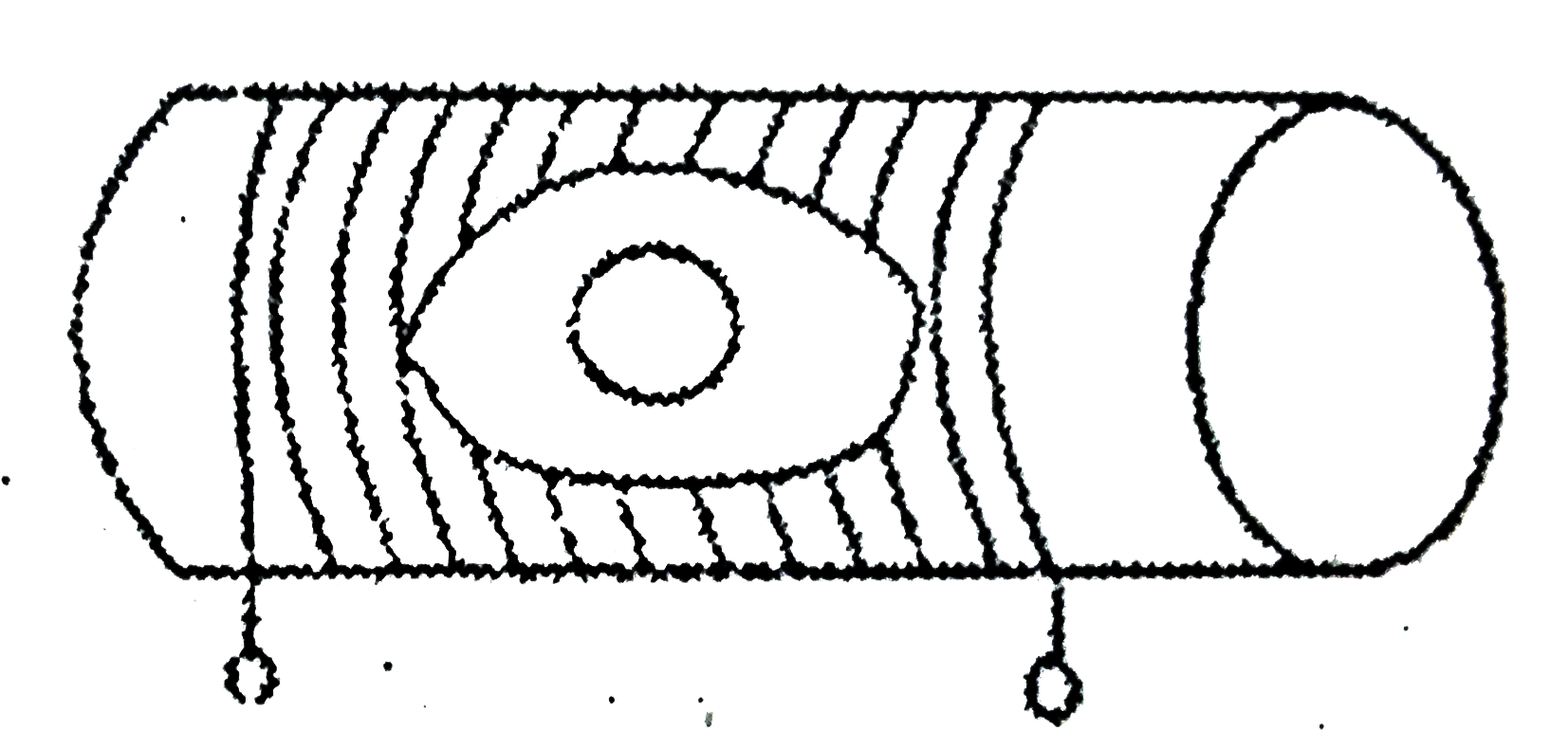
View SolutionA solenoid of length 20cm, area of cross- section 4.0cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross - sectional area 8.0cm2 and length 10cm. Find the mutual inductance between the solenoids.
View SolutionA solenoid 30 cm long is made by winding 2000 loops of wire on an iron rod whose cross-section is 1.5cm2. If the relative permeability of the iron is 600. what is the self-inductance of the solenoid?
View Solution(a) Calculate the self-inductance of a solenoid that is tightly wound with wire of diameter 0.10cm, has a cross-sectional area 0.90cm2 and is 40cm long
(b) If the current through the solenoid decreases uniformly from 10 A to 0A in 0.10s, what is the emf induced between the ends of the solenoid?
View SolutionWhen the number of turns and the length of the solenoid are doubled keeping the area of cross-section same, the inductance
View SolutionA solenoid has 2000 turns would over a length of 0.30 m. The area of its cross-section is 1.2×10−3m2. If an initial current of 2 A in the solenoid is reversed in 0.25 s, then the emf induced in the coil is
View Solution
