n = 5 , ms=+12 How many orbitals are possible :
25
30
50
35
The correct Answer is:A
To determine how many orbitals are possible when n=5 and ms=+12, we can follow these steps:
Step 1: Identify the Principal Quantum Number
The principal quantum number n indicates the shell number. Here, n=5 means we are dealing with the fifth shell.
Step 2: Calculate the Azimuthal Quantum Number l
The azimuthal quantum number l can take values from 0 to n−1. Therefore, for n=5:
- l can be 0,1,2,3,4.
Step 3: Determine the Number of Orbitals for Each l
The number of orbitals corresponding to each l value can be calculated using the formula:
Number of orbitals=2l+1
Now, we will calculate this for each value of l:
- For l=0 (s orbital):
2(0)+1=1 orbital
- For l=1 (p orbital):
2(1)+1=3 orbitals
- For l=2 (d orbital):
2(2)+1=5 orbitals
- For l=3 (f orbital):
2(3)+1=7 orbitals
- For l=4 (g orbital):
2(4)+1=9 orbitals
Step 4: Sum the Total Number of Orbitals
Now, we will add the number of orbitals from all l values:
1 (s)+3 (p)+5 (d)+7 (f)+9 (g)=25 orbitals
Conclusion
Thus, the total number of orbitals possible when n=5 is 25.
---
The principal quantum number n indicates the shell number. Here, n=5 means we are dealing with the fifth shell.
The azimuthal quantum number l can take values from 0 to n−1. Therefore, for n=5:
- l can be 0,1,2,3,4.
The number of orbitals corresponding to each l value can be calculated using the formula:
Number of orbitals=2l+1
Now, we will calculate this for each value of l:
- For l=0 (s orbital):
2(0)+1=1 orbital
- For l=1 (p orbital):
2(1)+1=3 orbitals
- For l=2 (d orbital):
2(2)+1=5 orbitals
- For l=3 (f orbital):
2(3)+1=7 orbitals
- For l=4 (g orbital):
2(4)+1=9 orbitals
Now, we will add the number of orbitals from all l values:
1 (s)+3 (p)+5 (d)+7 (f)+9 (g)=25 orbitals
Thus, the total number of orbitals possible when n=5 is 25.
Topper's Solved these Questions
Similar Questions
How many orbitals are possible for n = 3, l=2 ?
View SolutionHow many orbitals are possible in
5th energy level
View SolutionHow many methyl hexane are possible :
View SolutionHow many stereoisomers are possible for
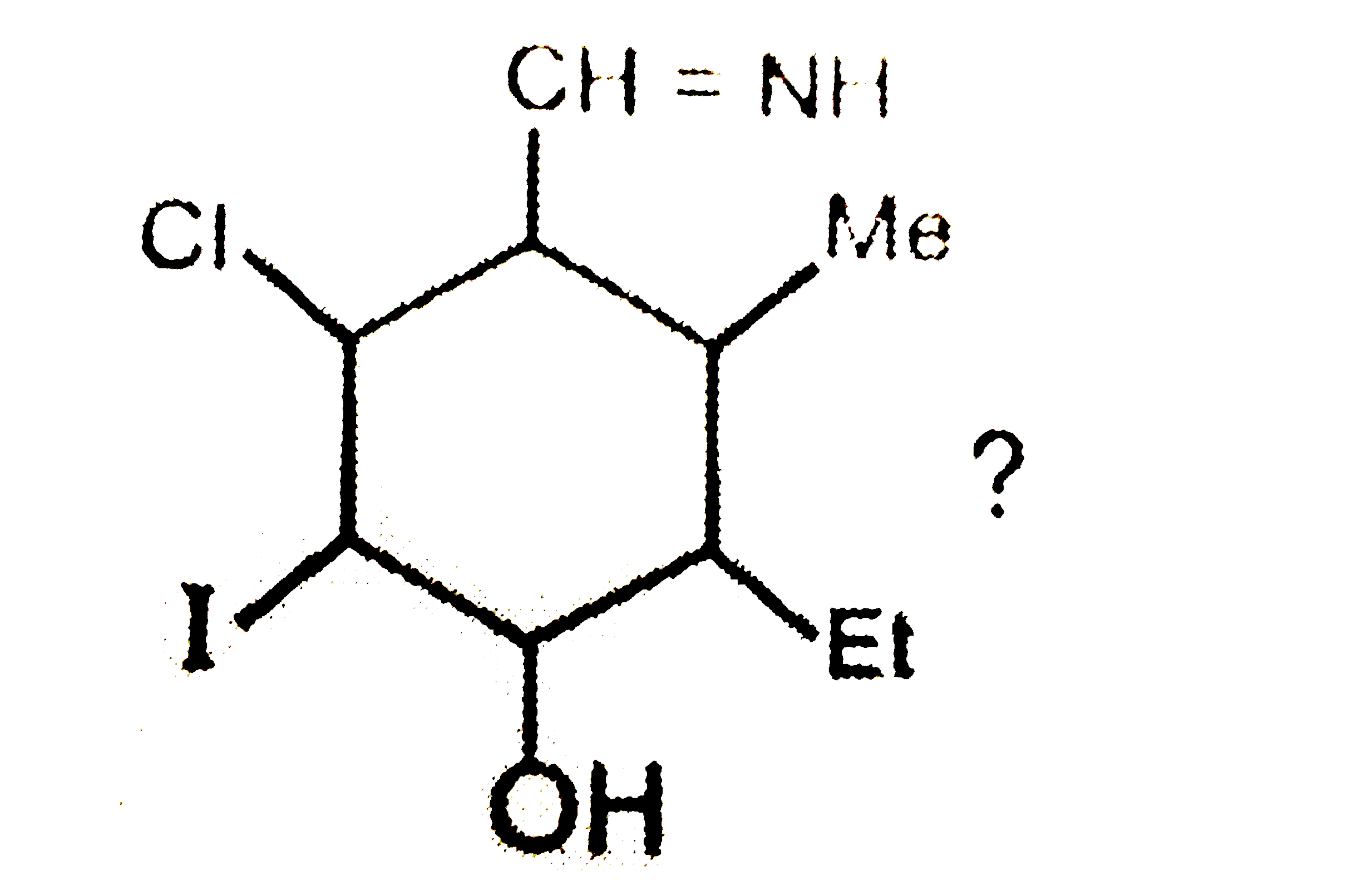
View SolutionHow many structures for F are possible
 .
.
View SolutionHow many geometrical isomers are possible for

View SolutionHow many tetramethyl benzene are possible:
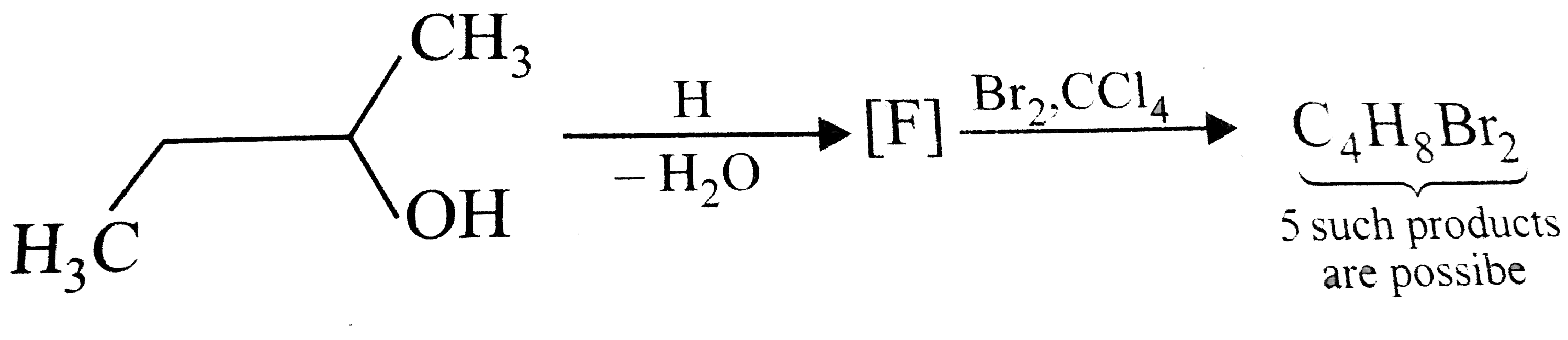
View Solution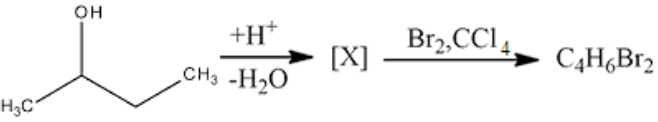
How many structures of X is possible ?
View Solution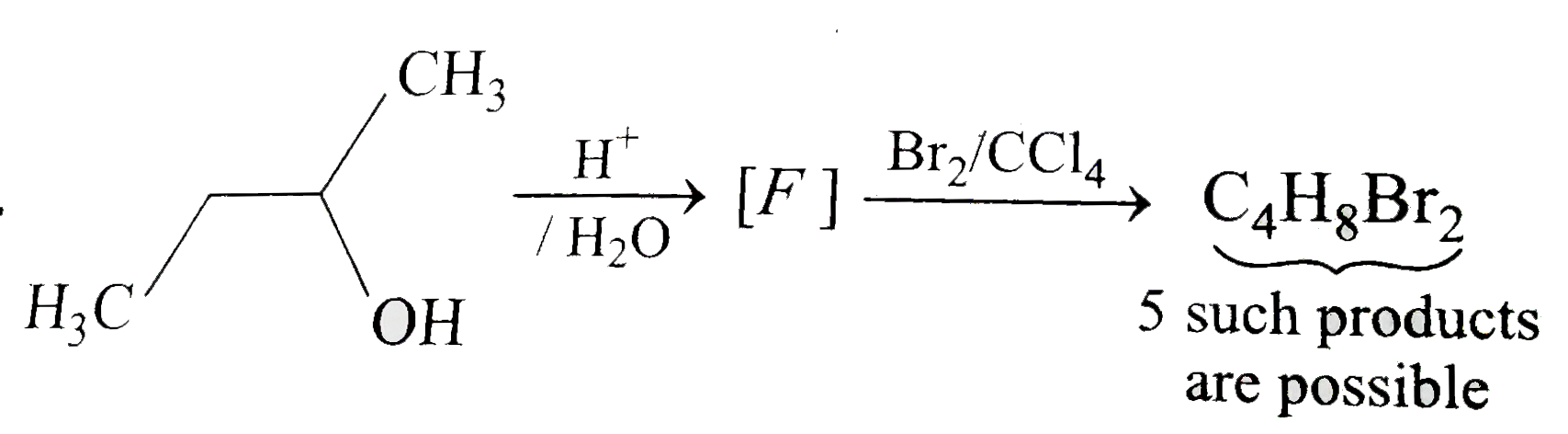
How many structures of F is possible?
View SolutionWhich of the following orbitals are possible ?
1s,2s,3f,3d
View Solution
