If temperature changes from 27∘C→42∘C then no. of molecules having energy greater than thershold energy become five times, then find activation energy of reaction in KJ. Given ln 5= 1.6094
The correct Answer is:84.30J
To solve the problem, we will use the Arrhenius equation and the information provided about the change in temperature and the increase in the number of molecules with energy greater than the threshold energy.
1. Convert Temperatures to Kelvin:
- Initial temperature T1=27∘C=27+273=300K
- Final temperature T2=42∘C=42+273=315K
2. Understand the Relationship Between Rate Constants:
- The problem states that the number of molecules with energy greater than the threshold energy becomes five times. Therefore, the rate constant K2 at the final temperature is:
K2=5K1
3. Write the Arrhenius Equation for Both Temperatures:
- For T1:
K1=Ae−EaRT1
- For T2:
K2=Ae−EaRT2
4. Substituting K2 into the Equation:
- Substitute K2=5K1 into the second equation:
5K1=Ae−EaRT2
- Now, we can write:
5Ae−EaRT1=Ae−EaRT2
5. Dividing Both Sides by A:
- Since A is a common factor, we can cancel it out:
5e−EaRT1=e−EaRT2
6. Taking Natural Logarithm on Both Sides:
- Taking the natural logarithm gives:
ln(5)=−EaRT2+EaRT1
- Rearranging gives:
ln(5)=EaR(1T1−1T2)
7. Substituting Known Values:
- We know ln(5)=1.6094, R=8.314J/(mol⋅K), T1=300K, and T2=315K:
1.6094=Ea8.314(1300−1315)
8. Calculating 1300−1315:
- Finding a common denominator (which is 94500):
1300−1315=315−30094500=1594500=16300
9. Substituting Back to Find Ea:
- Now substituting back:
1.6094=Ea8.314⋅16300
- Rearranging gives:
Ea=1.6094⋅8.314⋅6300
10. Calculating Ea:
- Performing the multiplication:
Ea=1.6094⋅8.314⋅6300≈84.297kJ
Final Answer:
The activation energy Ea is approximately 84.297 kJ.
- Initial temperature T1=27∘C=27+273=300K
- Final temperature T2=42∘C=42+273=315K
- The problem states that the number of molecules with energy greater than the threshold energy becomes five times. Therefore, the rate constant K2 at the final temperature is:
K2=5K1
- For T1:
K1=Ae−EaRT1
- For T2:
K2=Ae−EaRT2
- Substitute K2=5K1 into the second equation:
5K1=Ae−EaRT2
- Now, we can write:
5Ae−EaRT1=Ae−EaRT2
- Since A is a common factor, we can cancel it out:
5e−EaRT1=e−EaRT2
- Taking the natural logarithm gives:
ln(5)=−EaRT2+EaRT1
- Rearranging gives:
ln(5)=EaR(1T1−1T2)
- We know ln(5)=1.6094, R=8.314J/(mol⋅K), T1=300K, and T2=315K:
1.6094=Ea8.314(1300−1315)
- Finding a common denominator (which is 94500):
1300−1315=315−30094500=1594500=16300
- Now substituting back:
1.6094=Ea8.314⋅16300
- Rearranging gives:
Ea=1.6094⋅8.314⋅6300
- Performing the multiplication:
Ea=1.6094⋅8.314⋅6300≈84.297kJ
The activation energy Ea is approximately 84.297 kJ.
Similar Questions
If the rate of a reaction gets doubled as the temperature is increased from 27∘ to 37∘C. Find the activation energy of reaction?
View SolutionThe number of molecules with energy greater than tha threshold enegy for a reaction increases five fold by a rise of temperature from 27∘C to 42∘C. Its energy of activation in J/mol is ___________. (Take ln5=1.6094,R=8.314 J mol−1K−1)
View Solution
Knowledge Check
- Question 1 - Select One
As the temperature is raised from 20∘C to 40∘C, the average kinetic energy of neon atoms changes by a factor of which of the following?
A12B√313293C313293D2
The rate of a reaction triples when temperature changes from 20∘C to 50∘C. Calculate the energy of activation.
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
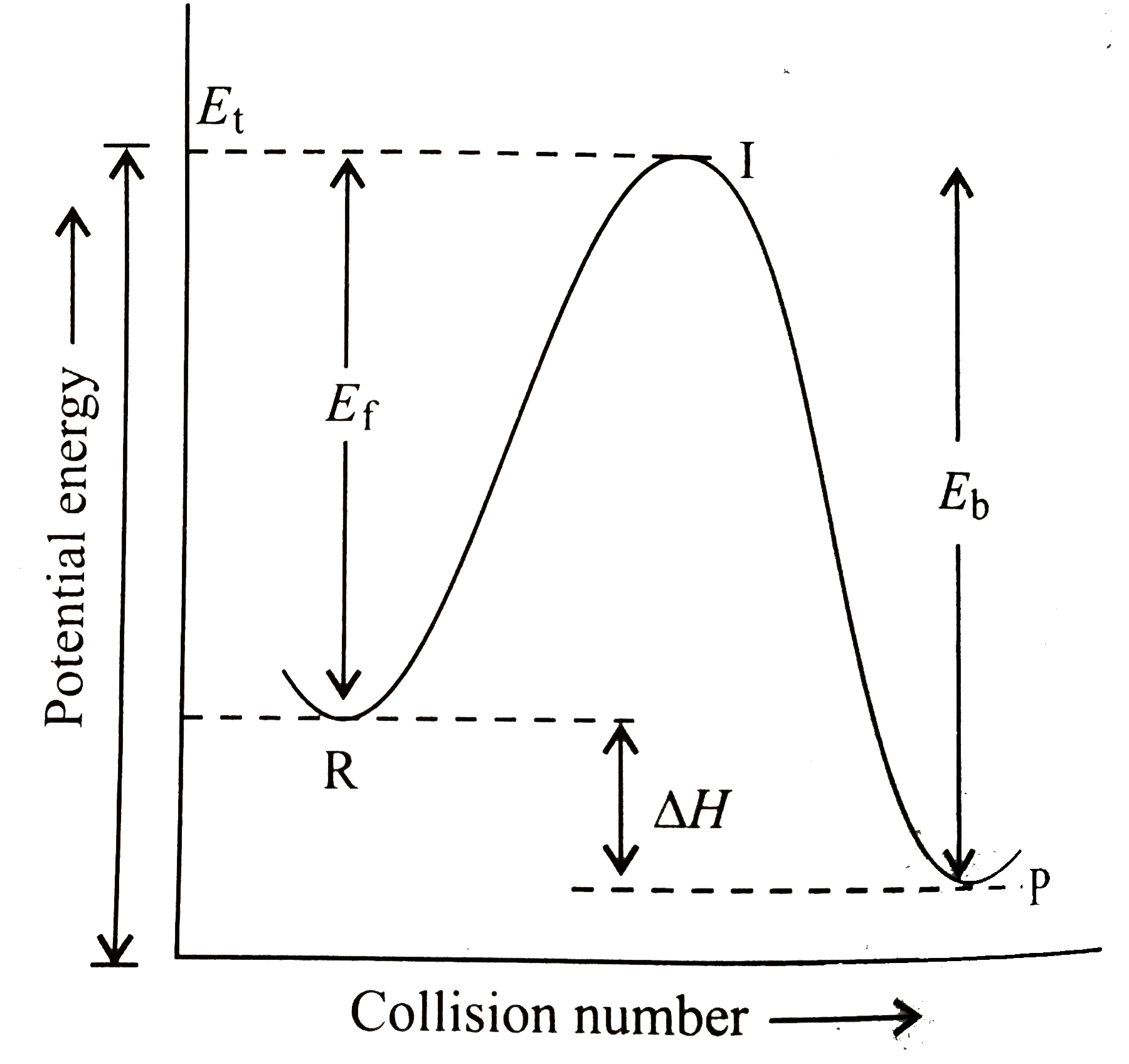
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
If a reaction A+B→C is exothermic to the extent 30kJmol−1 and the forward reaction has an activation energy of 249kJmol−1 the activation energy for reverse reaction in kJmol−1 isView SolutionThe rate of a reaction quadruples when the temperature changes from 300 to 310 K. The activation energy of this reaction is :
( Assume Activation energy and pre-exponential factor are independent of temperature, ln(2)=0.693,R=8.314J−mol−1K−1)View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.

Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
In a hypothetical reaction A→B, the activation energies for the forward and backward reactions are 15 and 9kJmol−1, respectively. The potential energy of A is 10kJmol−1. Which of the following is wrong?View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.

Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
The activation eneries for forward and backward reactions in a chemical reaction are 30.5 and 45.4kJmol−1 respectively. The reaction isView SolutionFor the first order reaction A→B+C , carried out at 27∘C if 3.8×10−16% of the reactant molecules exists in the activated state, the Ea (activation energy) of the reaction is :
View SolutionThe rate of a reaction becomes 4 times when temperature is raised from 293 K to 313 K. The activation energy for such reaction would be
View Solution

