Considering that Δ0>P, the magnetic moment (in BM) of [Ru(H2O)6]2+ would be _________.
To solve the problem regarding the magnetic moment of the complex (Ru(H2O)6)2+, we will follow these steps:
Step 1: Determine the Oxidation State of Ruthenium (Ru)
The complex (Ru(H2O)6)2+ has an overall charge of +2. Since water (H2O) is a neutral ligand, the oxidation state of Ru can be calculated as follows:
Let the oxidation state of Ru be x. The equation is:
x+6(0)=+2
Thus, x=+2.
Hint: Remember that neutral ligands do not contribute to the charge of the complex.
Step 2: Write the Electronic Configuration of Ruthenium
The atomic number of Ru is 44. The electronic configuration of Ru in its neutral state is:
(Kr)4d75s1
Since we are considering Ru in the +2 oxidation state, we need to remove 2 electrons. The electrons are removed from the highest energy level first, which is the 5s orbital, followed by the 4d orbital.
Removing 2 electrons gives us:
(Kr)4d6
Hint: When determining the electronic configuration for a cation, always remove electrons from the outermost shell first.
Step 3: Analyze the D-Orbital Splitting in an Octahedral Field
In an octahedral field, the d-orbitals split into two sets: t2g (lower energy) and eg (higher energy). The splitting can be represented as follows:
- t2g: 3 orbitals (lower energy)
- eg: 2 orbitals (higher energy)
Since Δ0>P (where Δ0 is the octahedral splitting energy and P is the pairing energy), this indicates that the electrons will pair up in the lower energy t2g orbitals before occupying the higher energy eg orbitals.
Hint: Remember that when Δ0 is greater than P, the complex will be low-spin, leading to pairing of electrons.
Step 4: Fill the Electrons in the d-Orbitals
With an electronic configuration of 4d6, we fill the electrons in the t2g orbitals first. Since we have 6 electrons, they will fill as follows:
- t2g: 6 electrons (fully filled)
- eg: 0 electrons
This results in all 6 electrons being paired in the t2g orbitals.
Hint: Count the number of unpaired electrons in the filled orbitals to determine the magnetic properties.
Step 5: Determine the Magnetic Moment
The magnetic moment (μ) can be calculated using the formula:
μ=√n(n+2)
where n is the number of unpaired electrons. Since all 6 electrons are paired, n=0.
Substituting n into the formula:
μ=√0(0+2)=√0=0 BM
Hint: A magnetic moment of zero indicates that the complex is diamagnetic.
Final Answer
The magnetic moment of (Ru(H2O)6)2+ is 0 BM.
The complex (Ru(H2O)6)2+ has an overall charge of +2. Since water (H2O) is a neutral ligand, the oxidation state of Ru can be calculated as follows:
x+6(0)=+2
Thus, x=+2.
The atomic number of Ru is 44. The electronic configuration of Ru in its neutral state is:
(Kr)4d75s1
Since we are considering Ru in the +2 oxidation state, we need to remove 2 electrons. The electrons are removed from the highest energy level first, which is the 5s orbital, followed by the 4d orbital.
(Kr)4d6
In an octahedral field, the d-orbitals split into two sets: t2g (lower energy) and eg (higher energy). The splitting can be represented as follows:
- eg: 2 orbitals (higher energy)
With an electronic configuration of 4d6, we fill the electrons in the t2g orbitals first. Since we have 6 electrons, they will fill as follows:
- eg: 0 electrons
The magnetic moment (μ) can be calculated using the formula:
μ=√n(n+2)
where n is the number of unpaired electrons. Since all 6 electrons are paired, n=0.
μ=√0(0+2)=√0=0 BM
The magnetic moment of (Ru(H2O)6)2+ is 0 BM.
Topper's Solved these Questions
Similar Questions
The magnetic moment of MnSO4.4H2O is:
View SolutionThe type of magnetism exhibited by [Mo(H2O)6]2+ ion is _______.
View SolutionThe type of magnetism exhibited by [Mn(H2O)6]2+ ion is ________ .
View SolutionConsider the reaction
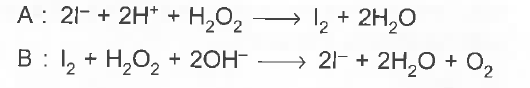
H2O2 is
View SolutionConsidering H2O as a weak field ligand, the number of unpaired electrons in [Mn(H2O)6]2+ will be (At. no. of Mn=25)
View Solution(a). Why Mn2+ compounds are more stable than Fe2+ towards oxidation to their +3 state?
(b). Calculate the magnetic moment of V3+ ion.
(c). [Ti(H2O)6_3+ gives violet coloured aqueous solution but
[Mg(H2O)6]2+ solution is colourless.
(d). [Ti(H2O)6]3+ is coloured whereas [Sc(H2O)6]3+ is colourless. Why?
View SolutionThe spin only magnetic moment value (in Bohr magneton unit) of [Cr(CO)6] is _____________ BM.
View Solutionthe pair of metal ions that can give a spin - only magnetic moment of 3.9 BM for the complex [M(H2O)6]Cl2is
View SolutionAmongst the following ions which one has the highest magnetic moment value?
(i). [Cr(H2O)6]3+
(ii). [Fe(H2O)6]2+
(iii). [Zn(H2O)]2+
View SolutionCalculate magnetic moment of Fe3+ in [Fe(CN)6]3+ and in [Fe(H2O)6]3+
View Solution
