একটি সরলরেখার বাইরের কোনো নির্দিষ্ট বিন্দু থেকে ওই সরলরেখার উপর □ (একটিই / একটির বেশি)লম্ব অঙ্কন করা যায় |
Step by step video & image solution for একটি সরলরেখার বাইরের কোনো নির্দিষ্ট বিন্দু থেকে ওই সরলরেখার উপর square (একটিই / একটির বেশি)লম্ব অঙ্কন করা যায় | by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Topper's Solved these Questions
- বিভিন্ন জ্যামিতিক চিত্র অঙ্কনBOOK - NCERT BANGLISH (BANGLISH MEDIUM)CHAPTER - বিভিন্ন জ্যামিতিক চিত্র অঙ্কনEXERCISE - EXERCISE
31 Videos
- বিজগানিতিক চলরাশির ধারণাBOOK - NCERT BANGLISH (BANGLISH MEDIUM)CHAPTER - বিজগানিতিক চলরাশির ধারণাEXERCISE - EXERCISE
60 Videos
- বৃত্ত বিষয়ক জ্যামিতিক ধারণাBOOK - NCERT BANGLISH (BANGLISH MEDIUM)CHAPTER - বৃত্ত বিষয়ক জ্যামিতিক ধারণাEXERCISE - EXERCISE
11 Videos
Similar Questions
স্কেল, পেনসিলের সাহায্যে AB একটি সরলরেখাংশ আঁক যার দৈর্ঘ্য 7 সেমি. | AB সরলরেখাংশের লম্ব-সমদ্বিখন্ডক অঙ্কন করো| স্কেল দিয়ে মেপে দেখো AB সরলরেখাংশের সমদ্বিখন্ডক অংশ দুটির দৈর্ঘ্য কত ?
View Solutionসংখ্যায় লেখ, 2-এর সাথে x- এর যোগফল
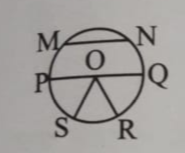
View Solutionবৃত্তের ছবি দেখো ও নিম্নের প্রশ্নটির উত্তর বার করোঃ O বিন্দু হল বৃত্তের □ । OQ সরলরেখাংশ হল বৃত্তের □ । PQ সরলরেখাংশ হল বৃত্তের □ ।OP সরলরেখাংশ হল বৃত্তের □ । MN সরলরেখাংশ হল বৃত্তের □ ।M ও N বিন্দু দুটি বৃত্তকে দুটি □ ভাগ করেছে।SR বৃত্তচাপ, SO ও RO ব্যাসার্ধ দ্বারা সীমাবদ্ধ বৃত্তাকার ক্ষেত্রের অংশ হল □ ।PQ ব্যাসের প্রান্তবিন্দু দুটি বৃত্তকে যে দুটি সমান অংশে ভাগ করে তাকে বলে □ ।
View Solutionভেক্টর পদ্ধতির প্রয়োগে দেখাও যে, (7,9),(3,−7) ও (-3,3) বিন্দু তিনটির সংযোগে একটি সমকোণী সমদ্বিবাহু ত্রিভুজ উৎপন্ন হয় |
View Solution1 থেকে 21 পর্যন্ত সংখ্যাগুলির মধ্য থেকে পরপর দুটি সংখ্যা তোলা হয়। প্রথমে তোলা সংখ্যাটি যুগ্ম এবং দ্বিতীয়বারে তোলা সংখ্যাটি অযুগ্ম হওয়ার সম্ভাবনা নির্ণয় করো যখন দ্বিতীয় সংখ্যাটি তোলার আগে প্রথম সংখ্যাটি (i) পুনঃস্থাপন করা হয় (ii) পুনঃস্থাপন করা হয় না।
View Solution20kg ভরের একটি বস্তুর ওপর (5+3x)N মানের একটি বল প্রযুক্ত করা হলো । এর ফলে বস্তুটি x অক্ষ বরাবর x=2m অবস্থান থেকে x =6 m স্থানে গেল। ওই বল দ্বারা বস্তুটির উপর কৃত কার্য
View SolutionCu_(1.7)S হল একটি ______________ যৌগ ।
View SolutionA_2(g)+B_2(g)
View SolutionCH_3MgI -কে ব্যবহার করে কীভাবে মিথক্সিইথেন তৈরি করা যায় ( শুধু তিরচিহ্ন দিয়ে সমীকরণ লেখাে ) ?
View Solutionএকটি LCR শ্রেণি সংযোগে R=400 Omega, L=100 mH এবং C= 1 muF। এই সংযোগকে 25sin2000t V মানের একটি তড়িৎ উৎসের সঙ্গে যোগ করা হল। (v) ব্যয়িত ক্ষমতা নির্ণয় করো।
View Solutionf(x)=x2−1x−1অপেক্ষকেরলেখচিত্রঅঙ্কনকরােএবংx = 1ওx= 2 বিন্দুতে অপেক্ষক সন্তত কি না তা লেখচিত্র থেকে বলাে।
View Solutionএকটি অপেক্ষক f(x)-এর নিম্নরূপ সংজ্ঞা দেওয়া হয় । f(x)={(x−1","যখন x>0),(−12","যখনx=0),(x+1","যখনx<0):}f(x)অপেক্ষকেরলেখচিত্রঅঙ্কনকরাে।লেখচিত্রথেকেf(x)অপেক্ষকেরx =-1/2বিন্দুতেমাননির্ণয়করােএবংx = 0বিন্দুতেf(x) সন্তত কি না বলে।
View Solutionx+y+1=0সরলরেখাস্থযেবিন্দু3x+4y +2 = 0-এর থেকে 1/5 একক দূরত্বে অবস্থিত সেই বিন্দুর স্থানাঙক হল—
View Solutionমনে করো xy সমতলে অবস্থিত S একটি বৃত্ত, যা x2+y2 = 4 সমীকরণ দ্বারা সংজ্ঞাত। মনে করো S বৃত্তের ওপর P এমন একটি বিন্দু যার স্থানাঙ্ক দুটি (x স্থানাঙ্ক ও yস্থানাঙ্ক) ধনাত্মক। মনে করো P বিন্দুতে S বৃত্তের স্পর্শক অক্ষদ্বয়কে M ও N বিন্দুতে ছেদ করেছে। তবে MN সরলরেখার মধ্যবিন্দু যে বক্রের ওপর অবস্থিত, তা হল—
View Solutionদেখাও যে, (-4,4, 4), (3,9, 4), (4, 5, 1) ও (0, -1,-1) বিন্দু চারটি একই সমতলে অবস্থিত।
View Solutionপ্রতিটি প্রশ্নে বিবৃতি-1 এবং বিবৃতি-2 দেওয়া আছে। প্রতিটি প্রশ্নের বিবৃতি দুটি নীচের কোন বিকল্পটিকে (A, B, C ও D-এর মধ্যে) সঠিকভাবে ব্যাখ্যা করে? সরলরেখা l:→r=ˆi−ˆj+ˆk+t(2ˆi+3ˆj−6ˆk) এবং সমতল p:→r.(2ˆi+3ˆj−6ˆk)=7। বিবৃতি−1সরলরেখাlসমতলp−কেএকটিঅনন্য(unique)বিন্দুতেছেদকরে।বিবৃতি−2l সরলরেখা p সমতলের ওপর লম্ব।
View Solution
