Find the dimensions of the quantity v in the equation,
v=πp(a2−x2)2ηl
where a is the radius and l is he length of the tube in which the fluid of coefficient of viscosity η is flowing , x is the distacne from the axis of the tube and p is the pressure differnece.
Step by step video & image solution for Find the dimensions of the quantity v in the equation, v=(pip(a^(2)-x^(2)))/(2etal) where a is the radius and l is he length of the tube in which the fluid of coefficient of viscosity eta is flowing , x is the distacne from the axis of the tube and p is the pressure differnece. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The dimensions of ab in the equation P=a2−t2bx where P is pressure, x is distance and t is time are
A[M2LT−3]B[ML0T−2]C[ML3T−1]D[M0LT−3]A physical quantity P=B2l2/m where B is the magnetic induction, l is the length and m is the mass. The dimensions of P is
AMLT−3BML2T−4I−2CM2L2T−4IDMLT−2I−2The velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
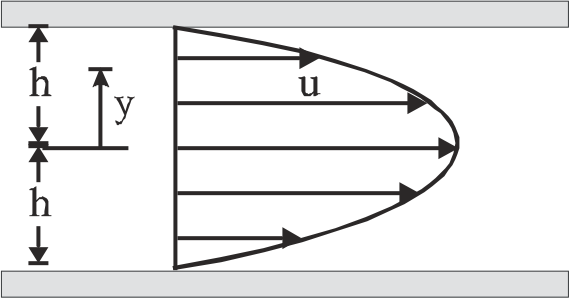
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Shear stress acting on the bottom wall isAτbottom wall=η(3Vh)Bτbottom wall=η(3V2h)Cτbottom wall=η(6Vh)Dτbottom wall=η(Vh)
A dimensionally consistent relation for the volume V of a liquid of coefficiet of viscosity η flowing per second through a tube of radius r and length l and having a pressure difference p across its end, is
View SolutionCheck the correctness of the relation : υ=πP(a2−x2)2ηI,
Whereυ is velocity, p is pressure difference, a is radius of tube, x is distance from the axis of tube, η is coeff. Of viscosity and I is length of the tube.
View SolutionA tube of length l and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The fluid flow velocity depends on the distance r from the axis of the tube as v=v0(1−r2/R2). Find:
(a) the volume of the fluid flowing across the section of the tube per unit time:
(b) the kinetic energy of the fluid within the tube's volume,
(c) the friction force exerted on the tube by the fluid,
(d) the pressure difference at the ends of the tube.
View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation

u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Consider a rectangular cross section of dimensions l x 2h as shown. The side AB is parallel to the plates. Volume flow rate through this cross section is
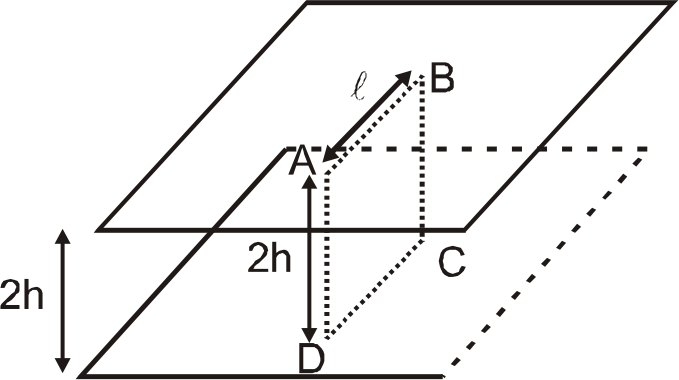
View SolutionStoke's law states that the viscous drag force F experienced by a sphere of radius a, moving with a speed v through a fluid with coefficient of viscosity η, is given by F=6πη If this fluid is flowing through a cylindrical pipe of radius r, length l and a pressure difference of P across its two ends, then the volume of water V which flows through the pipe in time t can be written as
Vt=K(pl)aηbrc
where k is a dimensionless constant. Correct values of a, b and c are -
View Solution
