Derive the following equations of motion for an object moving with constant acceleration along a straight line : v2=v20+2a(x−x0)=v20+2as
To derive the equation of motion v2=v20+2a(x−x0) for an object moving with constant acceleration along a straight line, we will follow these steps:
Step 1: Understand the Definitions
- Let v be the final velocity.
- Let v0 be the initial velocity.
- Let a be the constant acceleration.
- Let x be the final position.
- Let x0 be the initial position.
Step 2: Relate Acceleration to Velocity
Acceleration is defined as the rate of change of velocity with respect to time:
a=dvdt
Step 3: Relate Velocity to Position
Velocity can be defined as the rate of change of position with respect to time:
v=dxdt
Step 4: Rearranging the Equations
We can express acceleration in terms of position:
a=dvdt=dvdx⋅dxdt=vdvdx
This leads us to the equation:
adx=vdv
Step 5: Integrate Both Sides
Now we will integrate both sides. Since a is constant, we can take it out of the integral:
∫adx=∫vdv
The left side integrates to ax (from x0 to x), and the right side integrates to v22 (from v0 to v):
a(x−x0)=v22−v202
Step 6: Rearranging to Get the Final Equation
Now we can rearrange this equation:
2a(x−x0)=v2−v20
Adding v20 to both sides gives:
v2=v20+2a(x−x0)
Step 7: Simplifying the Equation
If we let s=x−x0 (the displacement), we can rewrite the equation as:
v2=v20+2as
Final Result
Thus, we have derived the equation of motion:
v2=v20+2a(x−x0)=v20+2as
- Let v be the final velocity.
- Let v0 be the initial velocity.
- Let a be the constant acceleration.
- Let x be the final position.
- Let x0 be the initial position.
Acceleration is defined as the rate of change of velocity with respect to time:
a=dvdt
Velocity can be defined as the rate of change of position with respect to time:
v=dxdt
We can express acceleration in terms of position:
a=dvdt=dvdx⋅dxdt=vdvdx
This leads us to the equation:
adx=vdv
Now we will integrate both sides. Since a is constant, we can take it out of the integral:
∫adx=∫vdv
The left side integrates to ax (from x0 to x), and the right side integrates to v22 (from v0 to v):
a(x−x0)=v22−v202
Now we can rearrange this equation:
2a(x−x0)=v2−v20
Adding v20 to both sides gives:
v2=v20+2a(x−x0)
If we let s=x−x0 (the displacement), we can rewrite the equation as:
v2=v20+2as
Thus, we have derived the equation of motion:
v2=v20+2a(x−x0)=v20+2as
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
For a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
A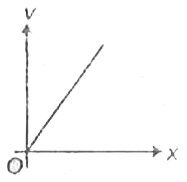 B
B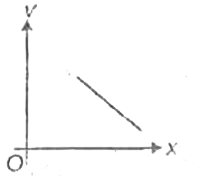 C
C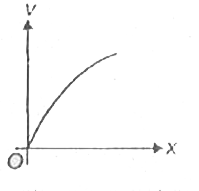 D
D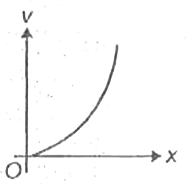
Prove that for a motion with a uniform rectilinear acceleration
2a(l−l0)=v2−v20View SolutionThe velocity v of moving object varies with displacement u as v=3x^(2)-2 ,then the acceleration at x=2m is
View SolutionA particle is moving in a straight line under constant acceleration alpha. If the intial velocity is v0, sketch the v-t and s-t graphs. (v0>0).
View SolutionThe velocity of a body moving in a straight line is given by v=(3x2+x)m/s . Find acceleration at x=2m.
View SolutionA particle confined to motion along an x axis moves with constant acceleration from x=2.0m to x=8.0 m during a 2.5 s time interval. The velocity of the particle at x=8.0m is 2.8 m/s. What is the constant acceleration during this time interval ?
View SolutionFigure depicts the motion of a particle moving along an x axis with a constant acceleration. What are the magnitude and direction of the particle's acceleration ? 8 6 4 2 0 2 3 t(s) -2
View SolutionAn aeroplane flying along the horizontal at a velocity v0 starts to ascend, describing a circle in the vertical plane. The velocity of the plane changes with height h above the initial level of motion according to the law v2=v20−2a0h. The velcity of the plane at the upper point of the trajectory is v1=v0/2. Determine the acceleration a of the plane at the moment when its velocity is directed vertically upwards.
View Solution

