Define relative velocity. Deduce an expression for relative velocity of one object with respect to another in terms of their velocities relative to the earth.
Step-by-Step Solution
1. Definition of Relative Velocity:
Relative velocity is defined as the velocity of one object as observed from another object. It is a measure of how fast one object is moving in relation to another.
2. Understanding the Concept:
If we have two objects, A and B, moving with velocities →vA and →vB respectively, we can describe the motion of A with respect to B.
3. Setting the Reference Frame:
To find the relative velocity of A with respect to B, we can consider B as a stationary observer. This means we are looking at how A moves from the perspective of B.
4. Expression for Relative Velocity:
The relative velocity of A with respect to B, denoted as →vAB, can be expressed using their velocities relative to a common reference point, which is the Earth in this case. The expression is given by:
→vAB=→vA−→vB
Here, →vA is the velocity of object A relative to the Earth, and →vB is the velocity of object B relative to the Earth.
5. Interpreting the Result:
This equation shows that the relative velocity of A with respect to B is simply the difference between the velocity of A and the velocity of B. If A is moving faster than B, then →vAB will be positive, indicating that A is moving away from B. Conversely, if B is moving faster than A, →vAB will be negative, indicating that A is moving towards B.
6. Relative Velocity of B with Respect to A:
Similarly, the relative velocity of B with respect to A can be expressed as:
→vBA=→vB−→vA
This shows how B perceives A's motion.
Relative velocity is defined as the velocity of one object as observed from another object. It is a measure of how fast one object is moving in relation to another.
If we have two objects, A and B, moving with velocities →vA and →vB respectively, we can describe the motion of A with respect to B.
To find the relative velocity of A with respect to B, we can consider B as a stationary observer. This means we are looking at how A moves from the perspective of B.
The relative velocity of A with respect to B, denoted as →vAB, can be expressed using their velocities relative to a common reference point, which is the Earth in this case. The expression is given by:
→vAB=→vA−→vB
Here, →vA is the velocity of object A relative to the Earth, and →vB is the velocity of object B relative to the Earth.
This equation shows that the relative velocity of A with respect to B is simply the difference between the velocity of A and the velocity of B. If A is moving faster than B, then →vAB will be positive, indicating that A is moving away from B. Conversely, if B is moving faster than A, →vAB will be negative, indicating that A is moving towards B.
Similarly, the relative velocity of B with respect to A can be expressed as:
→vBA=→vB−→vA
This shows how B perceives A's motion.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Velocity of geostationary satellite relative to the earth is
Asame as that of rotation of earth about its own axisBmore than that of the earth about its own axisC11.2 km/sDzero - Question 2 - Select One
The vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is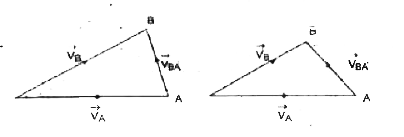
A70 km/hr towards EastB10 km/hr towards North EastC50 km/hr at some angle South of EastD50 km/hr at some angle North of East. - Question 3 - Select One
Assertion : The sound emitted by the source travels in all directions.
Reason : The relative velocity of sound with respect to the observer is the sum of velocity of sound and velocity of observer.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
Problems on Relative Velocity of Rain and Woman
View SolutionDefine relative refractive index in terms of velocity of light.
View SolutionIn perfectily inelastaic collition the relative velocity of the bodies
View SolutionIn two separate collisions, the coefficient of restitutions e1 and e2 are in the ratio 3:1. In the first collision the relative velocity of approach is twice the relative velocity of separation. Then, the ratio between relativevelocity of approach and relative velocity of separation in the second collision is
View SolutionWhat is the average velocity of H2 molecules at 100K relative to their velocity at 50K?
View Solution