Show the position vector for a particle in two dimensional motion. Write an expressionfor this position vector.
Step by step video & image solution for Show the position vector for a particle in two dimensional motion. Write an expressionfor this position vector. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - Motion in a PlaneEXERCISE - Example111videos
Motion in a Plane
- BOOK - SL ARORACHAPTER - Motion in a PlaneEXERCISE - Excercise397videos
Motion in a Plane
- BOOK - SL ARORACHAPTER - MECHANICSEXERCISE - Exercise341videos
MECHANICS
- BOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice66videos
MOTION IN ONE DIMENSION
Similar Questions
Knowledge Check
- Question 1 - Select One
Figure shows the position time graph for a particle in one dimensional motion. What is the displacement of the particle in first 4 seconds ?
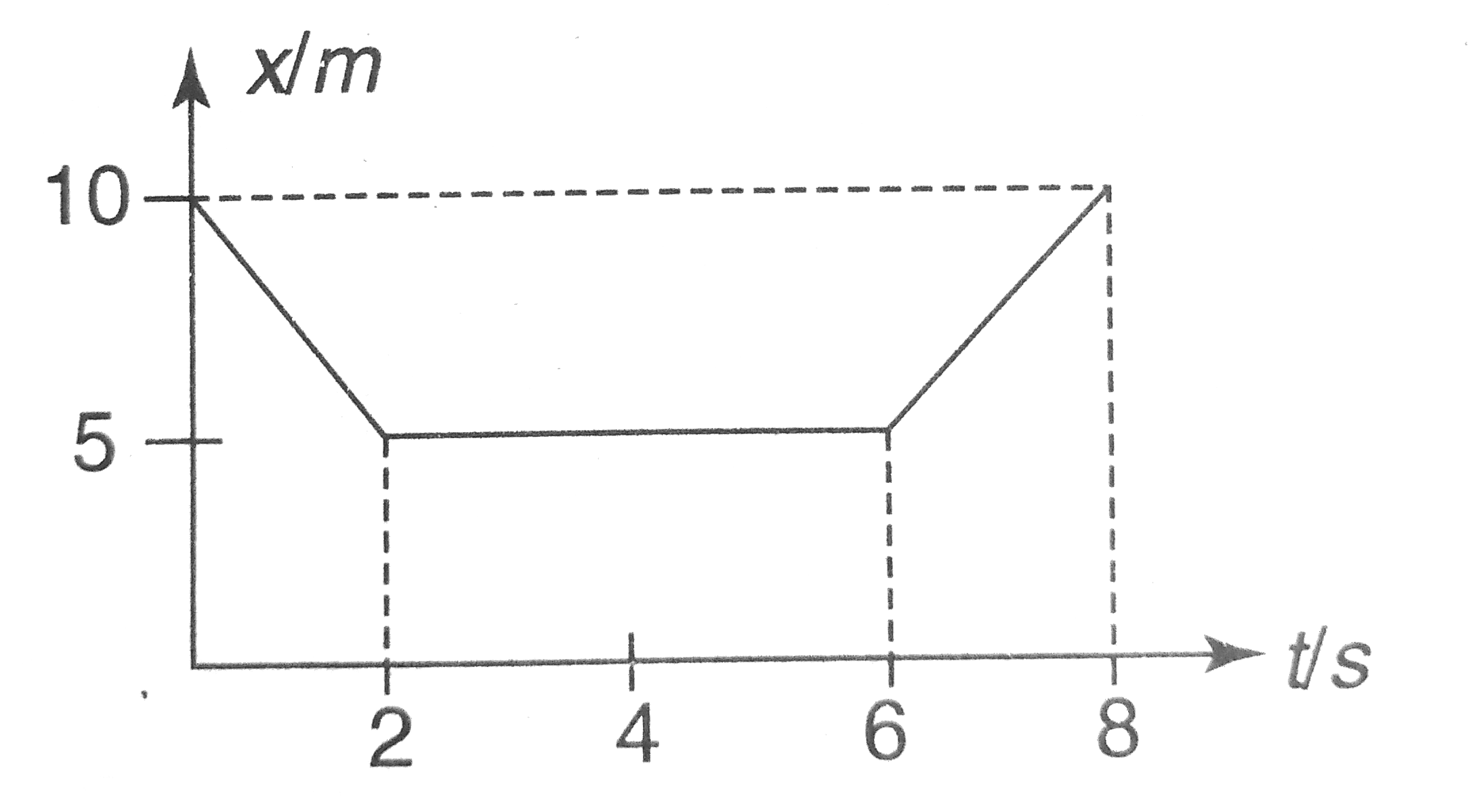 A5 mB−5mCzeroD15 m
A5 mB−5mCzeroD15 m - Question 2 - Select One
Figure shows the position the graph for a particle in one dimensional motion. Which of the graphs in fugure represent the variation in the velocity of the particle with time ?
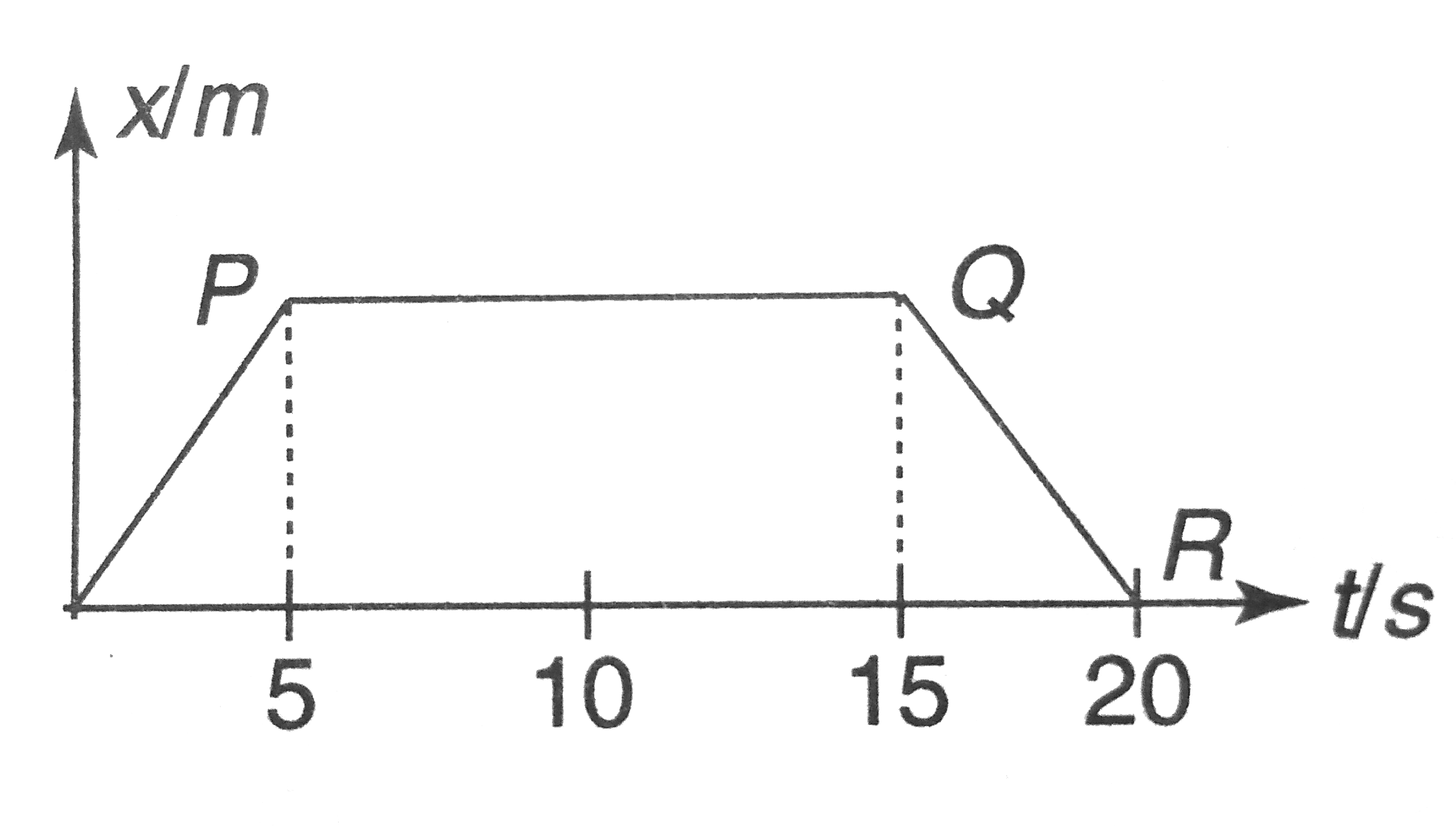 A
A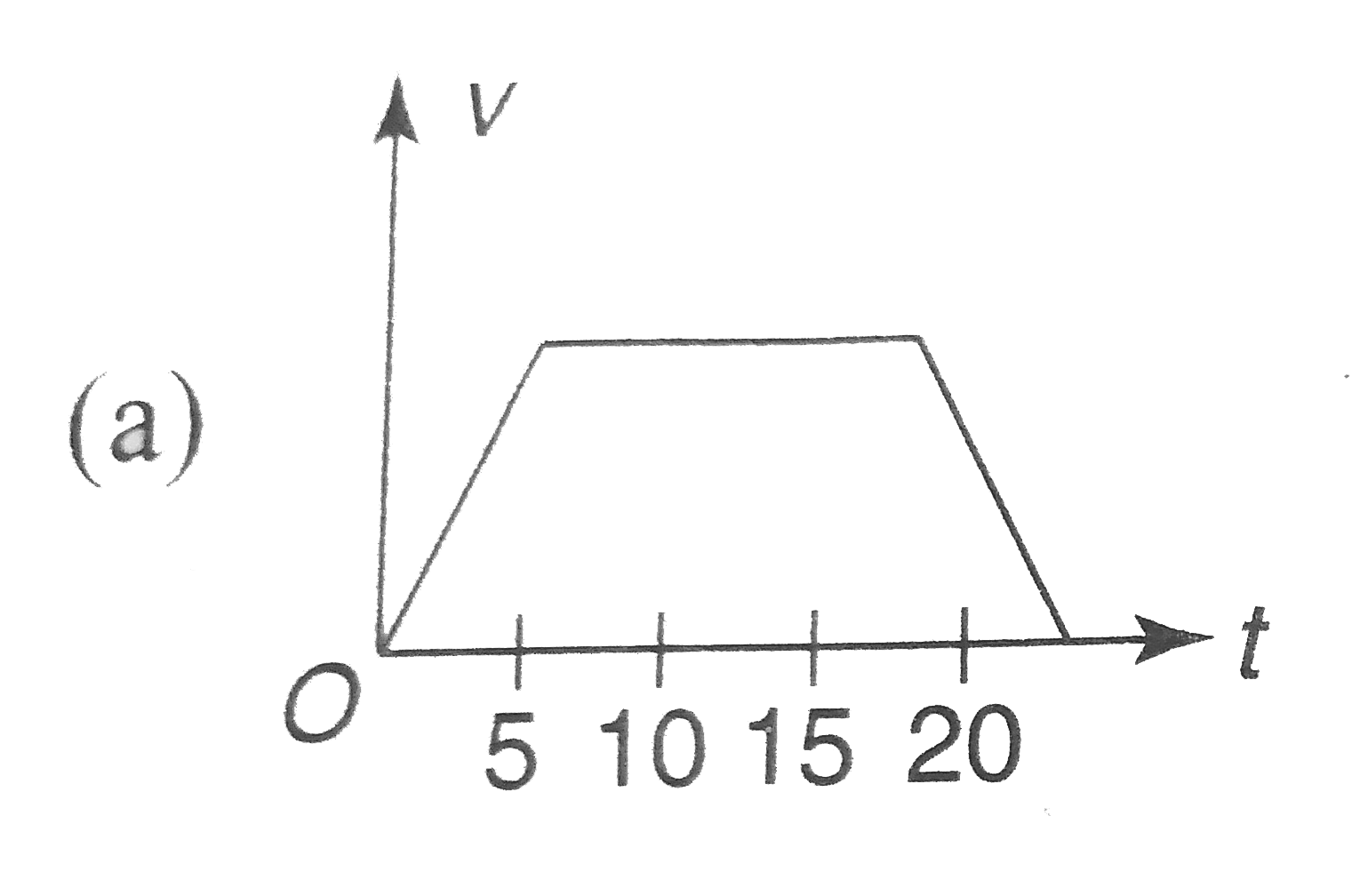 .B
.B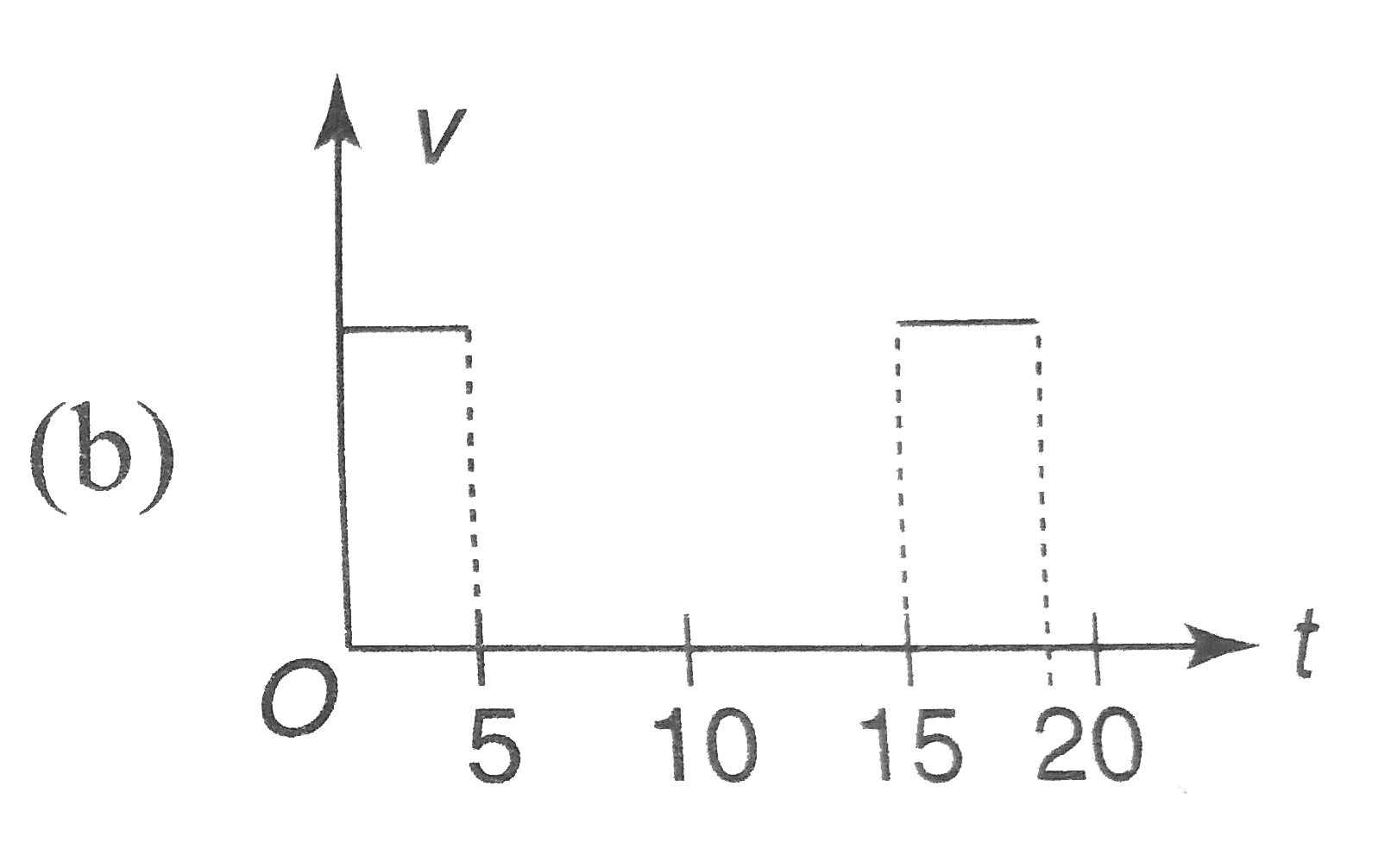 .C
.C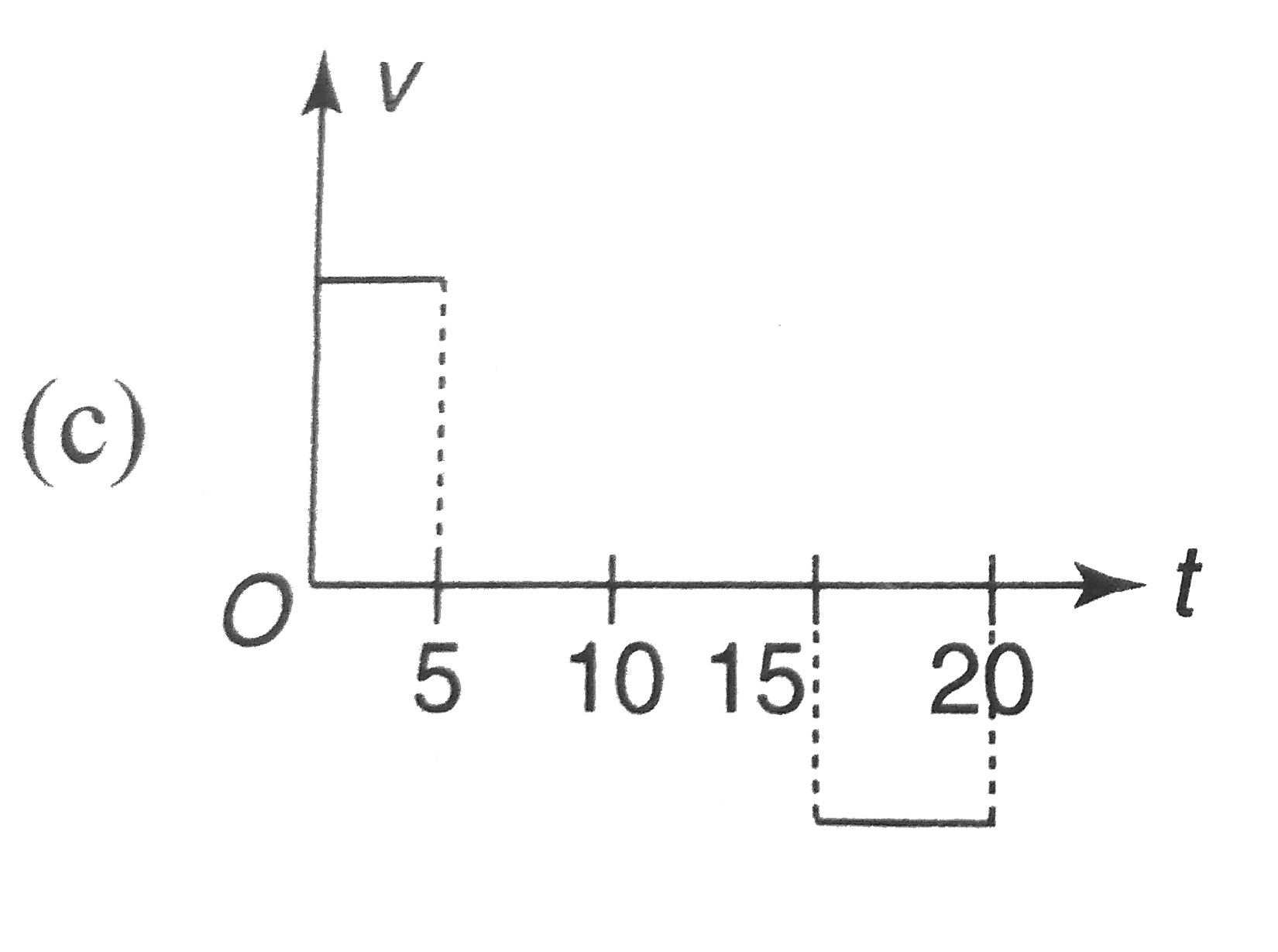 .D
.D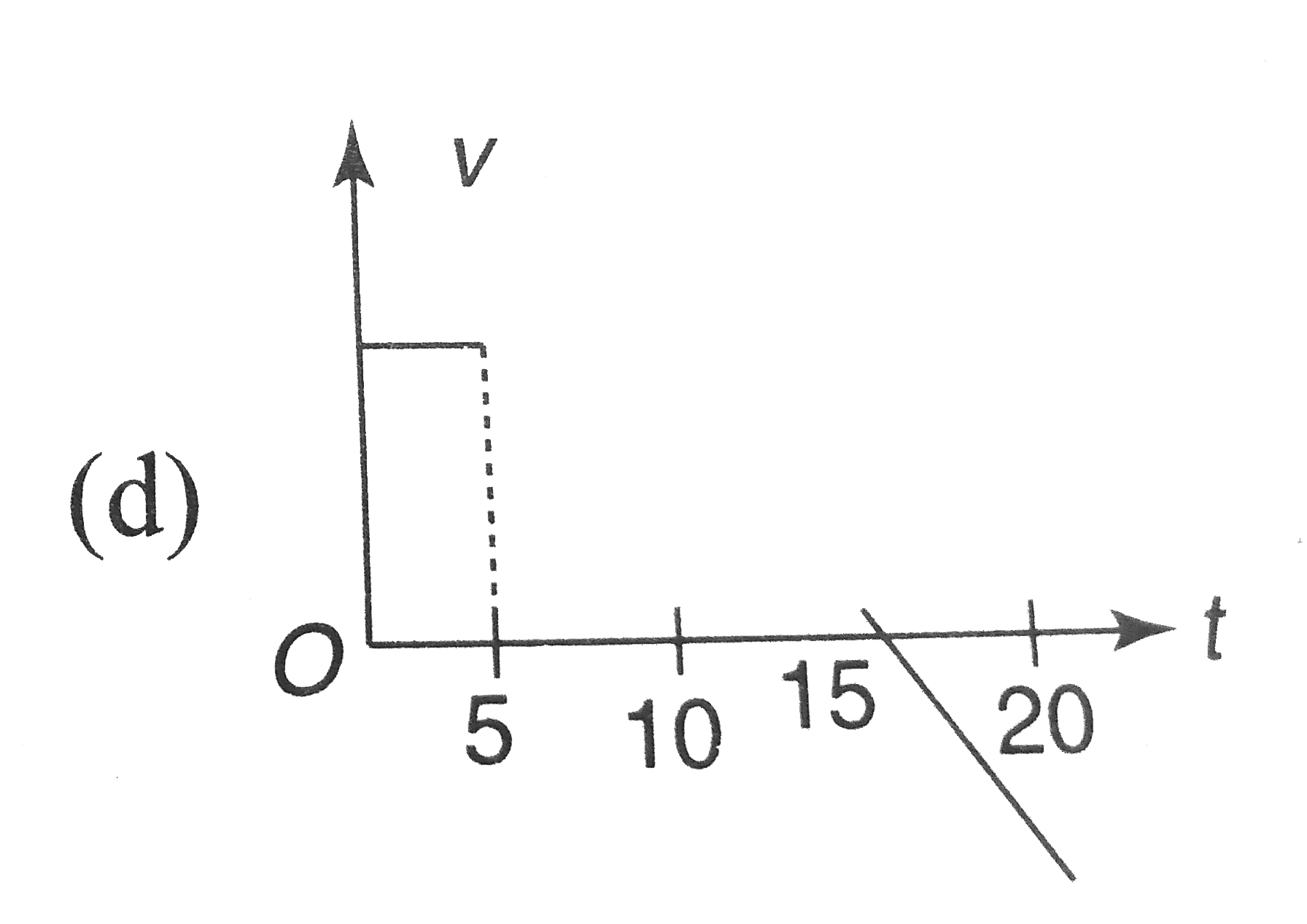 .
. - Question 3 - Select One
If the position vector of p is 3¯p+¯qand¯p divides PQ internally in the ratio 3:4, the position vector of Q is
A13(5¯p+4¯q)B13(4¯p+5¯q)C−13(5¯p+4¯q)D−13(4¯p+5¯q)
A particle is projected at an angle of 30∘w.r.t. horizontal with speed 20m/s:( use g=10m/s2)
(i) Find the position vector of the particle after 1s.
(ii) Find the angle between velocity vector and position vector at t=1s.View SolutionPosition vector in 2 dimensional plane and 3 dimensional plane
View SolutionShow that the horizontal vector and displacement vector in two dimensions .
View SolutionShow, by vector methods, that the angularbisectors of a triangle are concurrent and find an expression for the position vector of the point of concurrency in terms of the position vectors of the vertices.
View SolutionThe position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
View Solution


