A projectile is projected with velocity making angle with horizontal direction, find : time of flight.
To find the time of flight of a projectile projected with an initial velocity u at an angle θ with the horizontal, we can follow these steps:
1. Understand the Components of Velocity:
The initial velocity u can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
2. Analyze Vertical Motion:
The vertical motion of the projectile is influenced by gravity. The acceleration due to gravity g acts downward.
3. Use the Equation of Motion:
The vertical displacement y of the projectile can be described by the equation:
y=uyt−12gt2
Since the projectile returns to the same vertical level from which it was projected, the total vertical displacement y is zero at the time of flight T:
0=usinθ⋅T−12gT2
4. Rearranging the Equation:
Rearranging the equation gives:
12gT2=usinθ⋅T
Dividing both sides by T (where T≠0):
12gT=usinθ
5. Solving for Time of Flight T:
Now, solving for T:
T=2usinθg
Final Result:
The time of flight T of the projectile is given by:
T=2usinθg
The initial velocity u can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
The vertical motion of the projectile is influenced by gravity. The acceleration due to gravity g acts downward.
The vertical displacement y of the projectile can be described by the equation:
y=uyt−12gt2
Since the projectile returns to the same vertical level from which it was projected, the total vertical displacement y is zero at the time of flight T:
0=usinθ⋅T−12gT2
Rearranging the equation gives:
12gT2=usinθ⋅T
Dividing both sides by T (where T≠0):
12gT=usinθ
Now, solving for T:
T=2usinθg
The time of flight T of the projectile is given by:
T=2usinθg
Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
A2usinαgB2u2sinαgCusinαgDu2sinαgA projectile is projected with a velocity u at an angle θ with the horizontal. For a fixed θ, which of the graphs shown in the following figure shows the variation of range R versus u?
A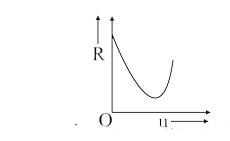 B
B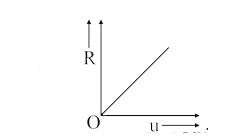 C
C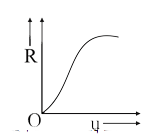 D
D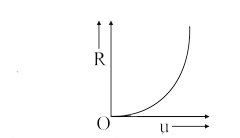
A projectile is thrown with velocity u making an angle θ with the horizontal. Its time of flight on the horizontal ground is 4 second. The projectile is moving at angle of 45∘ with the horizontal just one second after the projection. Hence the angle θ is (take g=10m/s2)
Atan−1(4)B60∘C53∘Dtan−1(2)
For a projectile first with velocity u at an angle θ with the horizontal.

View SolutionFind (a) time of flight , (b) Max.height (c ) Horizontal range of projectile projected with speed (v) making an angle θ with the horizontal direction from ground.
View SolutionIf a particle is projected with a velocity 49m/s making an angle 60∘ with the horizontal, its time of flight is
View SolutionIf a particle is projected with a velocity 49m/s making an angle 60∘ with the horizontal, its time of flight is
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
View Solution
