A solid of mass 2 kg moving with a velocity of strikes an ideal weightless spring and produces a compression of 25 cm in it. Calculate the force constant of the spring.
To solve the problem of calculating the force constant (k) of the spring when a solid mass strikes it, we can follow these steps:
Step 1: Understand the problem
We have a solid mass of 2 kg moving with a velocity of 10 m/s that strikes a weightless spring and compresses it by 25 cm. We need to find the spring constant (k).
Step 2: Convert units
First, we need to convert the compression of the spring from centimeters to meters:
- Compression (X) = 25 cm = 25/100 m = 0.25 m
Step 3: Use the conservation of energy principle
When the mass strikes the spring, its kinetic energy is converted into the potential energy stored in the spring at maximum compression. The equation for this is:
Kinetic Energy=Potential Energy of the spring
Step 4: Write the equations for kinetic and potential energy
The kinetic energy (KE) of the mass before it hits the spring is given by:
KE=12mv2
Where:
- m = mass = 2 kg
- v = velocity = 10 m/s
The potential energy (PE) stored in the spring when compressed is given by:
PE=12kX2
Where:
- k = spring constant (what we want to find)
- X = compression = 0.25 m
Step 5: Set the kinetic energy equal to the potential energy
Setting the two energies equal gives us:
12mv2=12kX2
Step 6: Simplify the equation
We can cancel the 12 from both sides:
mv2=kX2
Step 7: Substitute the known values
Substituting the values into the equation:
(2kg)(10m/s)2=k(0.25m)2
Calculating the left side:
2×100=k×0.0625
200=k×0.0625
Step 8: Solve for k
To find k, divide both sides by 0.0625:
k=2000.0625
Calculating this gives:
k=3200N/m
Final Answer
The force constant of the spring is k=3200N/m.
---
We have a solid mass of 2 kg moving with a velocity of 10 m/s that strikes a weightless spring and compresses it by 25 cm. We need to find the spring constant (k).
First, we need to convert the compression of the spring from centimeters to meters:
- Compression (X) = 25 cm = 25/100 m = 0.25 m
When the mass strikes the spring, its kinetic energy is converted into the potential energy stored in the spring at maximum compression. The equation for this is:
Kinetic Energy=Potential Energy of the spring
The kinetic energy (KE) of the mass before it hits the spring is given by:
KE=12mv2
Where:
- m = mass = 2 kg
- v = velocity = 10 m/s
PE=12kX2
Where:
- k = spring constant (what we want to find)
- X = compression = 0.25 m
Setting the two energies equal gives us:
12mv2=12kX2
We can cancel the 12 from both sides:
mv2=kX2
Substituting the values into the equation:
(2kg)(10m/s)2=k(0.25m)2
2×100=k×0.0625
200=k×0.0625
To find k, divide both sides by 0.0625:
k=2000.0625
k=3200N/m
The force constant of the spring is k=3200N/m.
Topper's Solved these Questions
Similar Questions
A 16kg block moving on a frictionless horiozntal surface with a velocity of 5cm−1 compreses an ideal spering and comes to rest. If the force constant of the spring be 100Nms−1, then how much is the spring compressed?
View SolutionA ball of mass 4kg, moving with a velocity of 10ms−1, collides with a spring of length 8m and force constant 100Nm−1. The length of the compressed spring is x m. The value of x, to the nearest integer, is ...........
View Solution
Knowledge Check
- Question 1 - Select One
When a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/mB100 N/mC150 N/mD200 N/m - Question 2 - Select One
A body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
A0.01 mB0.1mC0.2 mD0.5 m - Question 3 - Select One
A body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
A0.01 mB0.1 mC0.2 mD0.5 m
A 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
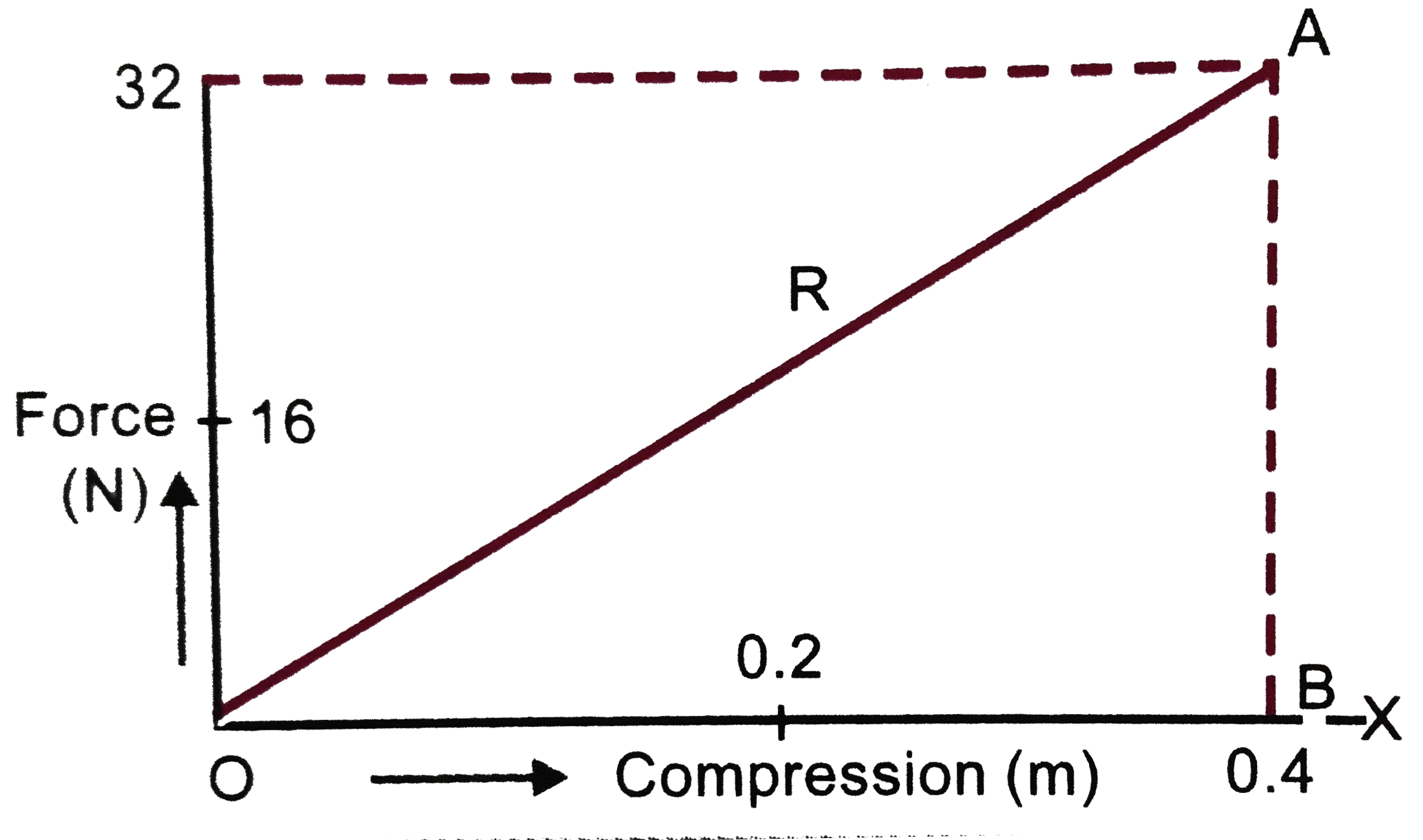
View SolutionFigure shows a force compression curve of a spring. A body of mass 5kg moving with the velocity of 8m/s hits the spring. Calculate the force constant of the spring and also the compression produced in the spring when the body hits it.
 View Solution
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be
 View Solution
View SolutionA block of mass 4kg slides on a horizontal frictionless surface with a speed of 2m/s. It is brought to rest in compressing a spring in its path. If the force constant of the spring is 400N/m, by how much the spring will be compressed
View Solution

