Extimate the amount of energy released in the following nuclear fusion reaction. 21H+21H→32He+10n Given mass of 21H=2.0141 amu, mass of 32He=3.0160 amu, mass of 10n=1.0087 amu and 1 amu =1.661×10−27kg. Express your answer in units of MeV?
To estimate the amount of energy released in the given nuclear fusion reaction, we will follow these steps:
Step 1: Write down the reaction and the masses involved.
The nuclear fusion reaction is:
21H+21H→32He+10n
The masses are given as:
- Mass of 21H=2.0141 amu
- Mass of 32He=3.0160 amu
- Mass of 10n=1.0087 amu
Step 2: Calculate the total mass of the reactants.
The total mass of the reactants (two hydrogen nuclei) is:
Total mass of reactants=2×mass of 21H=2×2.0141amu=4.0282amu
Step 3: Calculate the total mass of the products.
The total mass of the products (one helium nucleus and one neutron) is:
Total mass of products=mass of 32He+mass of 10n
=3.0160amu+1.0087amu=4.0247amu
Step 4: Calculate the mass defect.
The mass defect (Δm) is the difference between the total mass of the reactants and the total mass of the products:
Δm=Total mass of reactants−Total mass of products
=4.0282amu−4.0247amu=0.0035amu
Step 5: Convert the mass defect to energy.
Using Einstein's equation E=Δmc2, where c2 in terms of energy per mass in MeV is approximately 931.5MeV/amu:
E=Δm×931.5MeV/amu
=0.0035amu×931.5MeV/amu
=0.260MeV
Final Answer:
The amount of energy released in the nuclear fusion reaction is approximately 0.260 MeV.
---
The nuclear fusion reaction is:
21H+21H→32He+10n
- Mass of 21H=2.0141 amu
- Mass of 32He=3.0160 amu
- Mass of 10n=1.0087 amu
The total mass of the reactants (two hydrogen nuclei) is:
Total mass of reactants=2×mass of 21H=2×2.0141amu=4.0282amu
The total mass of the products (one helium nucleus and one neutron) is:
Total mass of products=mass of 32He+mass of 10n
=3.0160amu+1.0087amu=4.0247amu
The mass defect (Δm) is the difference between the total mass of the reactants and the total mass of the products:
Δm=Total mass of reactants−Total mass of products
=4.0282amu−4.0247amu=0.0035amu
Using Einstein's equation E=Δmc2, where c2 in terms of energy per mass in MeV is approximately 931.5MeV/amu:
E=Δm×931.5MeV/amu
=0.0035amu×931.5MeV/amu
=0.260MeV
The amount of energy released in the nuclear fusion reaction is approximately 0.260 MeV.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Energy released in the nuclear fusion reaction is :21H+31H→42He+10n
Atomic mass of 21H=2.014,31H=3.01642He=4.303,10n=1.009 (all in a.m.u.)A16.60 MeCB500 JC4×1067 KcalD8.30 eVIn the compound
1CH2=2CH−3CH2−4CH2−5C≡6CH
the 2C−3C bond is of the type :Asp−sp2Bsp3−sp3Csp−sp3Dsp2−sp3The end product of following reaction is
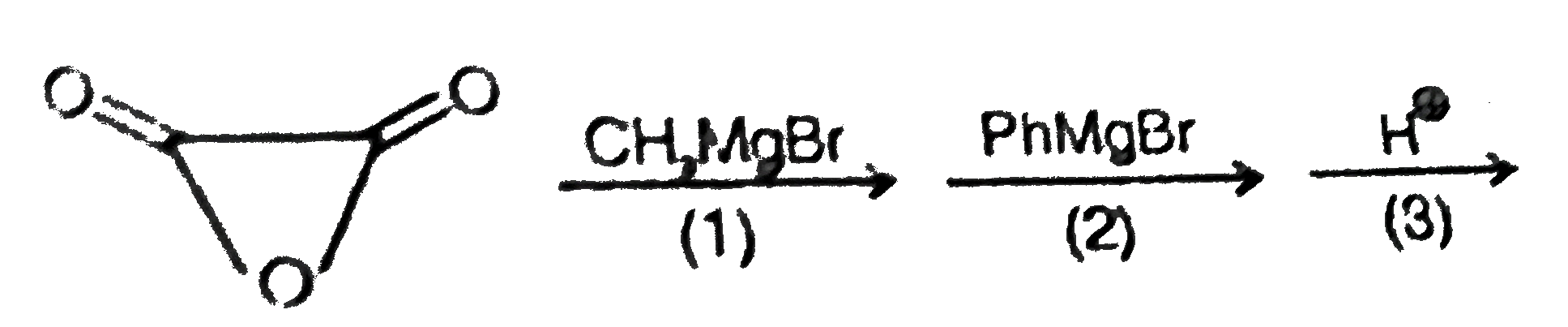
CH3MgBr−−−−−→(1)PhMgBr−−−−→(2)H⊕−−→(3)Aα,β-diketoneBα-Hydroxy acidC1,2-DiolDβ-Hydroxy acid
Estimate the amount of energy released in the nuclear fusion reaction:
_(1)H2+.1H2→.2He2+.0n1 Given that
M(.1H2)=2.0141u,M(.2He3)=3.0160u
mn=1.0087u ,
where 1u=1.661×10−27kg .
Express your answer in units of MeV.
View SolutionWhat is the hybridisatio carbon atoms numbered as 1,2 and 4 in the following molecule ?
H25C=4C=H3C−H22C−O∣∣C1−H
View SolutionH34C−O∣∣3 C−2CH2−O∣∣1 C−OH
View SolutionThe threshold energy (in (MeV) ) for the following nuclear reaction to proceed is
4H2e+underset(7)overset(14)N rarr 17O8+underset(1)overset(1)H<br><br>A→mic,massofunderset(2)overset(4)He = 4.00260 amuA→micmassofunderset(7)overset(14)N=14.00307 amuA→micmassofunderset(8)overset(17)Li=16.99913(aμ) Atomic mass of 1H1=1.00783(aμ)
View SolutionIn the following compound H−1C≡2C−3CH2−4CH3 the hybridization of C2 and C3 carbons are respectively .
View Solution
