A particle of mass m is initially at rest at the origin. It is subjected to a force and starts moving along the x-axis. It kinetic energy K changes with time as dK/dt=γt, where γ is a positive constant of appropriate dimensions. Which of the following statement is (are) true?
The force applied on the particle is constant.
The speed of the particle is proportional to time.
The distance of the particle from the origin increases linearly with time.
The force is conservative .
Step by step video & image solution for A particle of mass m is initially at rest at the origin. It is subjected to a force and starts moving along the x-axis. It kinetic energy K changes with time as dK//dt = gamma t, where gamma is a positive constant of appropriate dimensions. Which of the following statement is (are) true? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle moves along the x-axis with a position given by the equation x(t) = 5 + 3t, where x is in metres, and t is in seconds. The positive directions east. Which of the following statements about the particle is false ?
View SolutionA particle of mass m is at rest at the origin at time t=0. It is subjected to a force F(t)=F0e−bt in the X - direction. Its speed V(t) is depicted by which of the following curves.

View Solution
Knowledge Check
A particle free to move along the x-axis has potential energy given as
U(x)=k[1-exp(−x2)]for −∞≤+∞, where k is a positive constant of appropriate dimensions. Then :Aat points away from origin, the particles is in equilibriumBfor any finite non-zero value of x, there is a force directed away from the originCIts total mechanical energy is k/2 and it is equal to its equal to its kinetic energy at originDat x=0, the motion of the particle is simple harmonicA particle free to move along the x-axis has potential energy given as
U(x)=k[1-exp(−x2)]for −∞≤+∞, where k is a positive constant of appropriate dimensions. Then :Aat points away from origin, the particles is in equilibriumBfor any finite non-zero value of x, there is a force directed away from the originCIts total mechanical energy is k/2 and it is equal to its equal to its kinetic energy at originDat x=0, the motion of the particle is simple harmonicA particle free to move along the x−axis has potential energy given by U(x)=k[1−e−x2] for −∞≤x≤+∞, where k is a positive constant of appropriate dimensions. Then select the incorrect option
AAt point away from the origin, the particle is in unstable equilibriumBFor any finite non-zero value of x, there is a force directed away from the originCIf its total mechanical energy is k/2, it has its minimum kinetic energy at the originDFor small displacements from x = 0, the motion is simple harmonic
A particle of mass m is at rest at the origin at time t=0 It is subjected to a force F(t)=F0e−bt in the X-direction. Its speed V(t) is depicted by which of the following curves
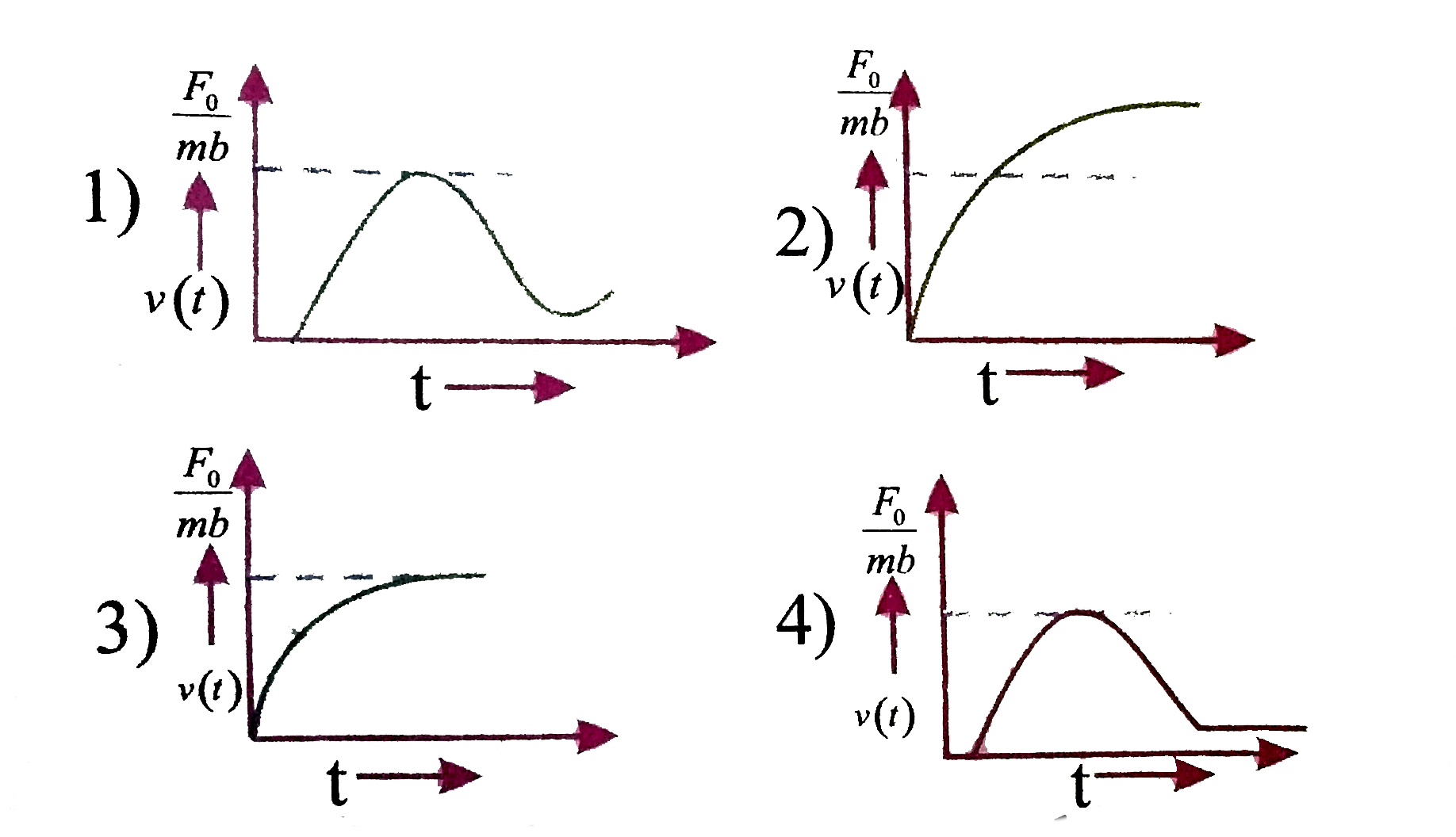
View SolutionAt time t=0s particle starts moving along the x− axis. If its kinetic energy increases uniformly with time 't', the net force acting on it must be proportional to
View SolutionA particle free to move along the (x - axis) hsd potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionA particle free to move along the (x - axis) hsd potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionThe velocity v of a particle of mass in moving along a straight line change within time t as d2vdt2=−Kv where K is a particle constant which of the following statement is correct?
View Solution
