A uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : the centre of mass
To determine the tangential velocity of the center of mass of a uniform circular disc of radius R that is rolling on a horizontal surface, we can follow these steps:
Step 1: Understand the Motion of the Disc
When a disc rolls without slipping, it has both translational and rotational motion. The center of mass of the disc moves forward while the disc rotates around its center.
Step 2: Identify the Relationship Between Linear and Angular Velocity
For a rolling disc, the relationship between the linear velocity (v) of the center of mass and the angular velocity (ω) is given by:
v=ωR
where R is the radius of the disc.
Step 3: Determine the Tangential Velocity at the Center of Mass
The tangential velocity of the center of mass is simply the linear velocity of the center of mass since the center of mass moves in a straight line. Therefore, the tangential velocity (v) at the center of mass is:
v=v
This means that the tangential velocity at the center of mass is equal to the translational velocity of the disc.
Step 4: Conclusion
Thus, the tangential velocity of the center of mass of the disc is:
v=v
where v is the translational velocity of the center of mass.
Final Answer
The tangential velocity of the center of mass of the uniform circular disc is equal to its translational velocity (v).
---
When a disc rolls without slipping, it has both translational and rotational motion. The center of mass of the disc moves forward while the disc rotates around its center.
For a rolling disc, the relationship between the linear velocity (v) of the center of mass and the angular velocity (ω) is given by:
v=ωR
where R is the radius of the disc.
The tangential velocity of the center of mass is simply the linear velocity of the center of mass since the center of mass moves in a straight line. Therefore, the tangential velocity (v) at the center of mass is:
v=v
This means that the tangential velocity at the center of mass is equal to the translational velocity of the disc.
Thus, the tangential velocity of the center of mass of the disc is:
v=v
where v is the translational velocity of the center of mass.
The tangential velocity of the center of mass of the uniform circular disc is equal to its translational velocity (v).
Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
A uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : at the upper most point
View SolutionA uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity (i) at the upper most point (ii) at the centre of mass and (iii) at the point of contact.
View Solution
Knowledge Check
A uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
 Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0
Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0A uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
 AmV202−mV20πBmv202+mv20πCmv202Dmv20
AmV202−mV20πBmv202+mv20πCmv202Dmv20A uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
 A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0r
A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0r
A uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
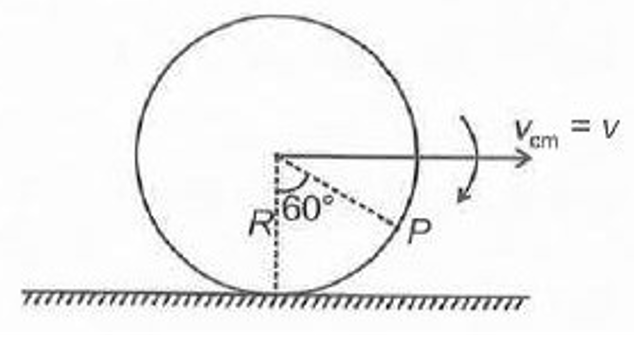
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View Solution
