Show that the area of the triangle contained between the vectors J and $ is one haif0fthe magnitude of →a×→b.
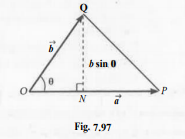
Step by step video & image solution for Show that the area of the triangle contained between the vectors J and $ is one haif0fthe magnitude of oversetrarraxxoversetrarrb. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
Knowledge Check
The angle between the vectors i-j+k and -i+j+2k is
A45∘B60∘C90∘D135∘The resultant of the vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between →A and →B is :-
A120∘B150∘C135∘DNone of theseTwo vectors of equal magnitude P are inclined at some angle such that the difference in magitude of resultant and magnitude of either of the vectors is 0.732 times either of the magnitude of vectors. If the angle between them is increased by half of its initial value then find the magnitude of difference of the vectors
A2PB√2PC3PD√3P
If the angle between two vectors of equal magnitude "P" is θ the magnitude of the difference of the vectors is
View SolutionIf the angle between two vectors of equal magnitude P is "theta" ,the magnitude of the difference of the vectors is
View SolutionThe resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -

View SolutionThe Vector area of the triangle whose adjacent sides are 2ˆi+3ˆj and −2ˆi+4ˆj is
View SolutionShow that if →u.d→udt=0 the vector →u is of constant magnitude.
View Solution
