Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is I. What is the moment of inertia about its diameter ?
I
I/2
I/√2
I+MR2
To find the moment of inertia of a ring of mass M and radius R about its diameter, we can use the perpendicular axis theorem. Let's go through the steps:
Step 1: Understand the Moment of Inertia about the Axis
The moment of inertia of a ring about an axis passing through the center and perpendicular to its plane is given as I.
Step 2: Apply the Perpendicular Axis Theorem
The perpendicular axis theorem states that for a planar body, the moment of inertia about an axis perpendicular to the plane (let's call it Iz) is equal to the sum of the moments of inertia about two perpendicular axes in the plane (let's call them Ix and Iy):
Iz=Ix+Iy
Step 3: Identify the Axes
For a ring:
- Iz is the moment of inertia about the axis perpendicular to the plane of the ring (which we know is I).
- Ix and Iy are the moments of inertia about the diameters in the plane of the ring.
Step 4: Use Symmetry
Due to the symmetry of the ring:
Ix=Iy
Let’s denote Ix=Iy=Id (the moment of inertia about the diameter).
Step 5: Substitute into the Perpendicular Axis Theorem
Substituting into the perpendicular axis theorem:
I=Ix+Iy=Id+Id=2Id
Step 6: Solve for Id
From the equation above, we can solve for Id:
Id=I2
Final Answer
Thus, the moment of inertia of the ring about its diameter is:
Id=I2
---
The moment of inertia of a ring about an axis passing through the center and perpendicular to its plane is given as I.
The perpendicular axis theorem states that for a planar body, the moment of inertia about an axis perpendicular to the plane (let's call it Iz) is equal to the sum of the moments of inertia about two perpendicular axes in the plane (let's call them Ix and Iy):
Iz=Ix+Iy
For a ring:
- Iz is the moment of inertia about the axis perpendicular to the plane of the ring (which we know is I).
- Ix and Iy are the moments of inertia about the diameters in the plane of the ring.
Due to the symmetry of the ring:
Ix=Iy
Let’s denote Ix=Iy=Id (the moment of inertia about the diameter).
Substituting into the perpendicular axis theorem:
I=Ix+Iy=Id+Id=2Id
From the equation above, we can solve for Id:
Id=I2
Thus, the moment of inertia of the ring about its diameter is:
Id=I2
Topper's Solved these Questions
- System of particles & rotational MotionBook:SL ARORAChapter:System of particles & rotational MotionExercise:EXERCISE
Explore 353 Videos
- ROTATIONAL MOTIONBook:SL ARORAChapter:ROTATIONAL MOTIONExercise:Problem for self practice
Explore 90 Videos
- Thermal Properties of MatterBook:SL ARORAChapter:Thermal Properties of MatterExercise:Exercise
Explore 449 Videos
Similar Questions
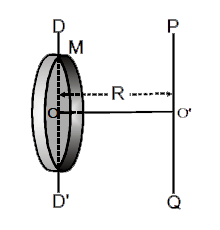
The moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionWhat is the moment of inertia of a ring of mass 2kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane ? Also find the moment of inertia about a parallel axis through its edge.
View Solution
Knowledge Check
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correct
The moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
View SolutionCalculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
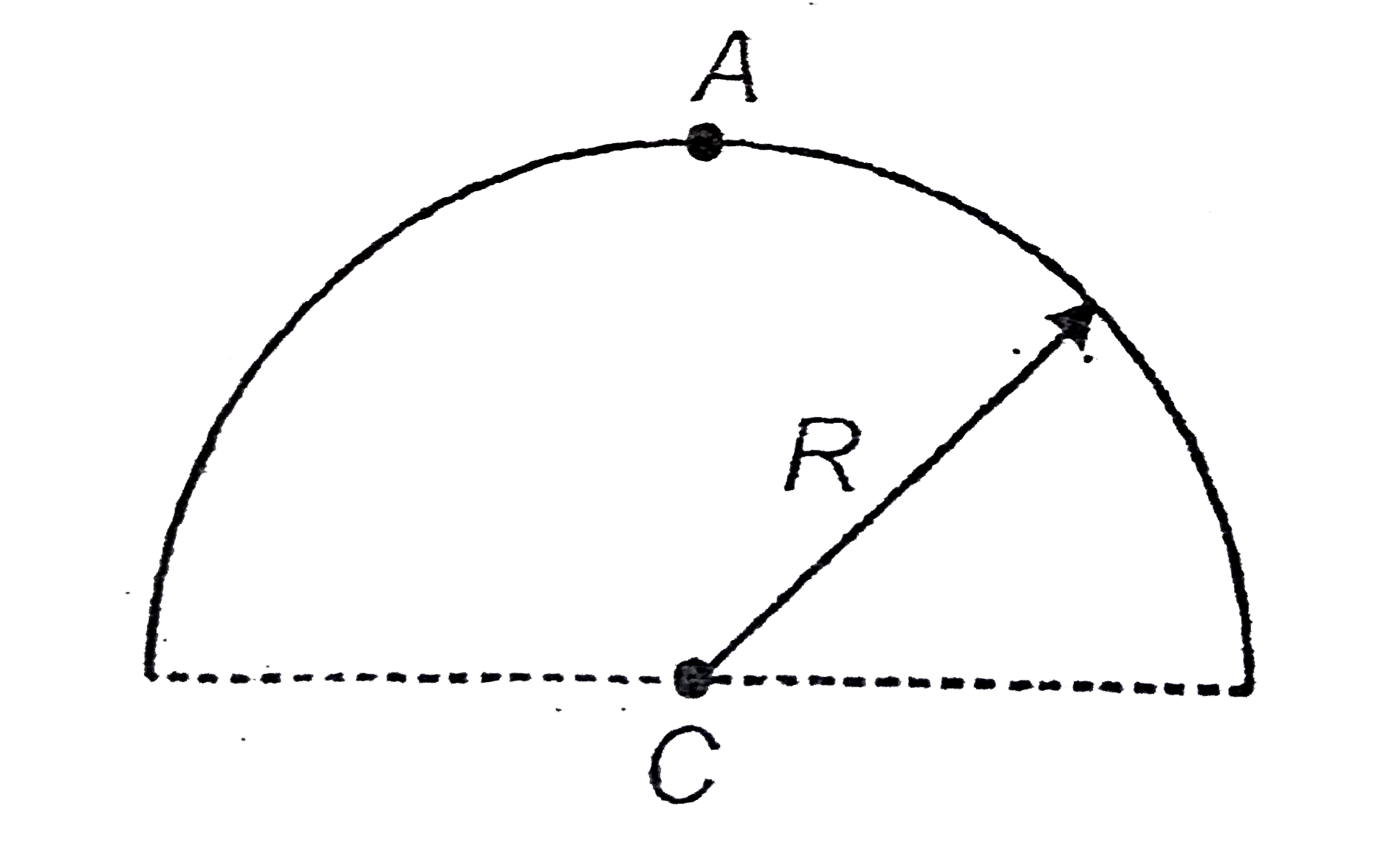
View SolutionMoment of inertia of a half ring of mass m and radius R about an axis passing through point A perpendicular to the plane of the paper is IA. If IC is the moment of inertia of the ring about an axis perpendicular to the plane of paper and passing through point C, then
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View Solution