Give the units and dimensions of gravitational field intensity.
To find the units and dimensions of gravitational field intensity, we can follow these steps:
Step 1: Understand the Definition
Gravitational field intensity (often denoted as →g) is defined as the gravitational force experienced by a unit mass placed in a gravitational field. Mathematically, it can be expressed as:
→g=→Fm
where →F is the gravitational force and m is the mass.
Step 2: Identify the Units of Force
The SI unit of force is the Newton (N). Therefore, we can write:
Unit of →F=N
Step 3: Identify the Units of Mass
The SI unit of mass is the kilogram (kg). Therefore, we can write:
Unit of m=kg
Step 4: Calculate the Units of Gravitational Field Intensity
Using the definition from Step 1, we can substitute the units of force and mass:
Unit of →g=Nkg=N/kg
Step 5: Convert Newton to Base Units
We know that:
1 N=1 kg⋅m/s2
Thus, we can express the unit of gravitational field intensity as:
Unit of →g=kg⋅m/s2kg=m/s2
Step 6: Find the Dimensions of Gravitational Field Intensity
To find the dimensions, we can use the dimensions of force and mass:
- The dimension of force →F is given by:
Dimension of →F=(M)(L)(T−2)
- The dimension of mass m is:
Dimension of m=(M)
Now, substituting into the formula for gravitational field intensity:
Dimension of →g=(M)(L)(T−2)(M)=(L)(T−2)
Final Answer
Thus, the units and dimensions of gravitational field intensity are:
- Units: N/kg or m/s²
- Dimensions: (L)(T^{-2})
---
Gravitational field intensity (often denoted as →g) is defined as the gravitational force experienced by a unit mass placed in a gravitational field. Mathematically, it can be expressed as:
→g=→Fm
where →F is the gravitational force and m is the mass.
The SI unit of force is the Newton (N). Therefore, we can write:
Unit of →F=N
The SI unit of mass is the kilogram (kg). Therefore, we can write:
Unit of m=kg
Using the definition from Step 1, we can substitute the units of force and mass:
Unit of →g=Nkg=N/kg
We know that:
1 N=1 kg⋅m/s2
Thus, we can express the unit of gravitational field intensity as:
Unit of →g=kg⋅m/s2kg=m/s2
To find the dimensions, we can use the dimensions of force and mass:
- The dimension of force →F is given by:
Dimension of →F=(M)(L)(T−2)
- The dimension of mass m is:
Dimension of m=(M)
Dimension of →g=(M)(L)(T−2)(M)=(L)(T−2)
Thus, the units and dimensions of gravitational field intensity are:
- Units: N/kg or m/s²
- Dimensions: (L)(T^{-2})
Topper's Solved these Questions
Similar Questions
Knowledge Check
The S.I. units of intensity of gravitational field
AJ/kgBJ/kgs2CN/kgDm/s3Dimensions of magnetic field intensity is
A[M0L−1T0A1]B[MLT−1A−1]C[ML0T−2A−1]D[MLT−2A]Assertion : Gravitational field is zero both at centre and infinity.
Reason : The dimensions of gravitational field is [LT−2]AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is false.DIf the assertion and reason both are false.
What is the unit of intensity of the gravitational field ?
View SolutionGravitational potential V versus distance r graph is represented in the figure. The magnitude of gravitational field intensity is equal to
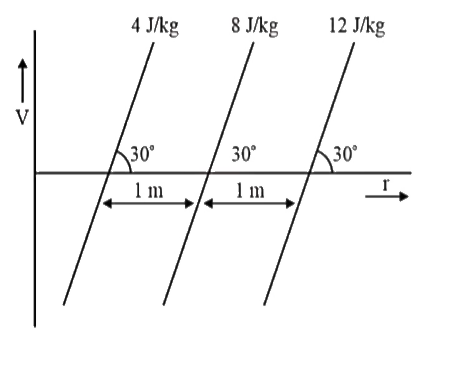
View SolutionState the dimensions of gravitational potential.
View SolutionGravitational force is a conservation and medium independent force. Its nature is attractive. Gravitational field intensity and gravitational potential gives information about gravitational fied in vector and scaler form respectively. Actually gravitational fied intensity is equal to the negative of the negative of teh potential gradient. potential energy is defined for only conservation force. it is also equal to the total energy in escaping condition. gravitational potential is either negative or zero but can never be positive due to attractive nature of gravitational force.
Gravitational potential versus distance r graph is represented in figure. The magnitude of gravitational field intensity is equal to

View SolutionThe dimensions of gravitational constant G are :
View Solution