Two soap bubbles of unequal sizes are blown at the end of a capillary tube. Which one will grow at the expense of the other end what does it show?
To solve the problem of which soap bubble will grow at the expense of the other when two bubbles of unequal sizes are blown at the end of a capillary tube, we can follow these steps:
Step 1: Understand the Concept of Excess Pressure in Bubbles
The excess pressure inside a soap bubble is given by the formula:
P=4Tr
where P is the excess pressure, T is the surface tension of the soap solution, and r is the radius of the bubble.
Step 2: Compare the Radii of the Bubbles
Let’s assume we have two bubbles:
- Bubble A (smaller bubble) with radius rA
- Bubble B (larger bubble) with radius rB
Since rA<rB, we can conclude that the excess pressure in Bubble A will be greater than that in Bubble B.
Step 3: Analyze the Excess Pressure
From the formula, we can see that:
- For Bubble A (smaller):
PA=4TrA
- For Bubble B (larger):
PB=4TrB
Since rA<rB, it follows that:
PA>PB
Step 4: Determine Which Bubble Will Grow
The bubble with the higher excess pressure (Bubble A) will lose air to the bubble with the lower excess pressure (Bubble B). Therefore, Bubble B will grow at the expense of Bubble A.
Step 5: Conclusion
Thus, the larger bubble (Bubble B) will grow at the expense of the smaller bubble (Bubble A). This phenomenon demonstrates the principle that in a system of bubbles, the smaller bubble tends to shrink while the larger bubble expands due to the differences in excess pressure.
Summary
- The smaller bubble has higher excess pressure.
- The larger bubble will grow at the expense of the smaller bubble.
The excess pressure inside a soap bubble is given by the formula:
P=4Tr
where P is the excess pressure, T is the surface tension of the soap solution, and r is the radius of the bubble.
Let’s assume we have two bubbles:
- Bubble A (smaller bubble) with radius rA
- Bubble B (larger bubble) with radius rB
From the formula, we can see that:
- For Bubble A (smaller):
PA=4TrA
- For Bubble B (larger):
PB=4TrB
PA>PB
The bubble with the higher excess pressure (Bubble A) will lose air to the bubble with the lower excess pressure (Bubble B). Therefore, Bubble B will grow at the expense of Bubble A.
Thus, the larger bubble (Bubble B) will grow at the expense of the smaller bubble (Bubble A). This phenomenon demonstrates the principle that in a system of bubbles, the smaller bubble tends to shrink while the larger bubble expands due to the differences in excess pressure.
- The smaller bubble has higher excess pressure.
- The larger bubble will grow at the expense of the smaller bubble.
Topper's Solved these Questions
- Mechanical Properties of fluidsBOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise
459 Videos
- Mathematical toolsBOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise
20 Videos
- Mechanical Properties of SolidsBOOK - SL ARORACHAPTER - Mechanical Properties of SolidsEXERCISE - Example
113 Videos
Similar Questions
A soap bubble is blown at the end of a capillary tube of radius a and length L. When the other end is left open, the bubble begins to deflate. Write the radius of the bubble as a function of time if the initial radius of the bubble was R0. Surface tension of soap solution is T. It is known that volume flow rate through a tube of radius a and length L is given by Poiseuille’s equation- Q=πa4ΔP8≠L

Where ΔP is pressure difference at the two ends of the tube and ≠ is coefficient of viscosity. Assume that the bubble remains spherical.
View SolutionTwo soap bubbles A and B of different diameters are blown at the two ends of a bent tube. By opening the stopcock S, the two bubbles are put in communication. What will happen?
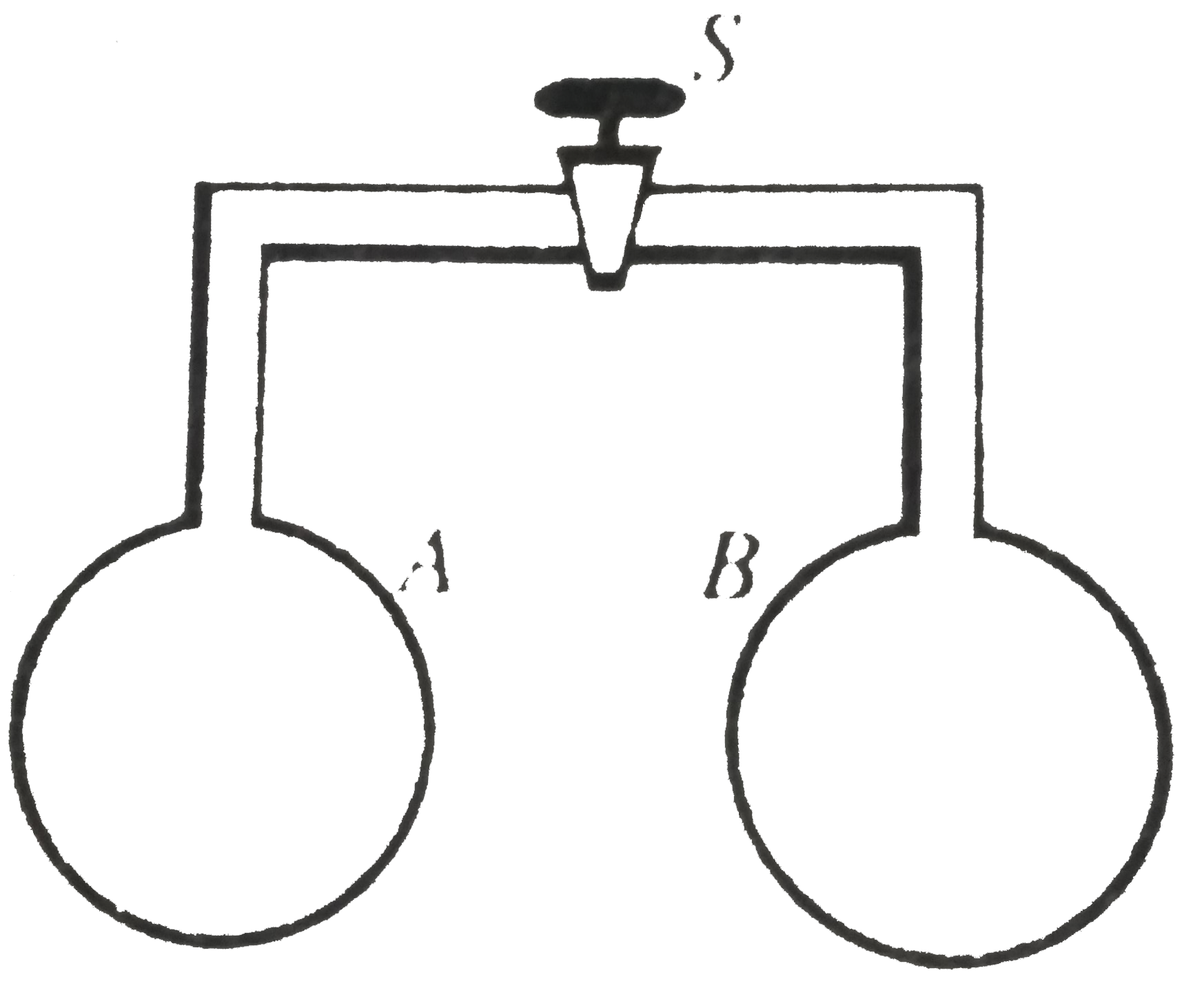
View Solution
Knowledge Check
When one end of a capillary tube is dipped vertically in water, the pressure below the meniscus of water is
Amore than upper side pressureBlesser than upper side pressureCequal to atmosphericDequal to upper side pressureIf two soap bubbles of unequal radii are in communication with each other , then
Aair flows from the larger bubble into smaller bubble unitl they have the same size .Bthe size of the bubbles remains the same .Cair flows from smaller bubble into larger bubble and the larger bubble grows in size and the size of the smaller bubble decreases.Dair may flow from the smaller to larger bubble or from larger to smaller bubble depending upon the concentration of the soap solution.Two unequal soap bubbles are formed one on each side of a tube closed in the middle by a tap. What happens when the tap is opened to put the two bubbles in communication?
Aair flows from the bigger bubble to the smaller bubble till the sizes become equalBair flows from bigger bubble to the smaller bubble till their sizes are interchangedCair flows from the smaller bubble to the larger bubbleDthere is no flow of air
Explain why water would completely fill a fine capillary tube which is open at both ends when one end is immersed in water.
View SolutionThe soap bubble formed at the end of the tube is blown very slowly. Draw the graph between excess of pressure inside the bubble with time.
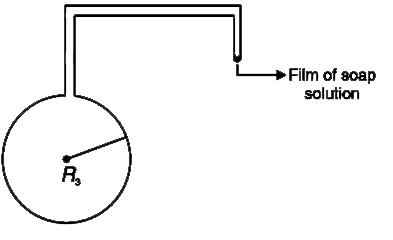
View SolutionIn the last problem, one of the bubbles supplies its entire air to the other bubble and a film of soap solution is formed at the end of the straw which keeps it closed. What is the radius of curvature of this film if the bigger bubble has grown in size and its radius has become R3.
View SolutionTow soap bubbles A and B are formed at the two open ends of a tube. The bubble A is smaller then bubble B. If the valve on the tube connecting the two bubbles is opened and air can flow freely between the bubbles, then
View SolutionThe locus of the centre of the cicle for which one end of a diamert is (1.) while the other end is one the line
View Solution
