For different capillaries of radiusr,the condition of liquid rise (h) above the liquid surface is
rh^2-constant
hrconstant
h+ r = constant
h r -constant
To solve the problem regarding the relationship between the capillary rise (h) and the radius (R) of different capillaries, we can follow these steps:
1. Understand the Capillary Rise Formula:
The formula for capillary rise is given by:
h=2Tcosθrρg
where:
- h = height of liquid rise
- T = surface tension of the liquid
- θ = contact angle
- r = radius of the capillary tube
- ρ = density of the liquid
- g = acceleration due to gravity
2. Identify Constant Parameters:
In this scenario, we can assume that the surface tension T, contact angle θ, density ρ, and gravitational acceleration g are constant for a given liquid and tube material.
3. Analyze the Relationship:
From the formula, we can see that the height of the liquid rise h is inversely proportional to the radius r:
h∝1r
This implies that if the radius r increases, the height h decreases, and vice versa.
4. Establish the Constant Product:
Since h is inversely proportional to r, we can express this relationship as:
h⋅r=constant
This means that the product of the height of the liquid rise and the radius of the tube remains constant for different capillary tubes.
5. Conclusion:
Therefore, the final relationship can be stated as:
h⋅R=k
where k is a constant.
Final Answer:
The condition of liquid rise h above the liquid surface for different capillaries of radius R is given by the relationship:
h⋅R=constant
The formula for capillary rise is given by:
h=2Tcosθrρg
where:
- h = height of liquid rise
- T = surface tension of the liquid
- θ = contact angle
- r = radius of the capillary tube
- ρ = density of the liquid
- g = acceleration due to gravity
In this scenario, we can assume that the surface tension T, contact angle θ, density ρ, and gravitational acceleration g are constant for a given liquid and tube material.
From the formula, we can see that the height of the liquid rise h is inversely proportional to the radius r:
h∝1r
This implies that if the radius r increases, the height h decreases, and vice versa.
Since h is inversely proportional to r, we can express this relationship as:
h⋅r=constant
This means that the product of the height of the liquid rise and the radius of the tube remains constant for different capillary tubes.
Therefore, the final relationship can be stated as:
h⋅R=k
where k is a constant.
The condition of liquid rise h above the liquid surface for different capillaries of radius R is given by the relationship:
h⋅R=constant
Topper's Solved these Questions
- Mechanical Properties of fluidsBOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise
459 Videos
- Mathematical toolsBOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise
20 Videos
- Mechanical Properties of SolidsBOOK - SL ARORACHAPTER - Mechanical Properties of SolidsEXERCISE - Example
113 Videos
Similar Questions
When a capillary tube of radius r is immersed in a liquid of density ρ, the liquid rises to a height h in it. If m is the mass of the liquid in the capillary tube, find the potential energy of this mass of the liquid in the tube.
View SolutionDue to capillary action, a liquid will rise in a tube, if the angle of contact is
View Solution
Knowledge Check
When two capillary tubes of different diameters are dipped vertically in a liquid , the rise of the liquid in the capillary tube
Ais same in both tubesBis more in tube of larger diameterCis more in tube of smaller diameterDthere is no rise of liquid in capillary tube of larger diameter.A liquid rises in a capillary tube of radius r upto height h and tha mass of liquid is 20 gm . If a the radius of capillary tube is half and height is twice , then the new mass of a liquid will be ,
A10 gmB80 gmC20 gmD40 gmWith the rise of temperature ,the surface tension of liquid :
AincreasesBdecreasesCremains unchangedDnone of these
Due to capillary action, a liquid will rise in a tube, if the angle of contact is
View Solution
A container is partially filled with a liquid of density ρ2 A capillary tube of radius r is vertically inserted in this liquid. Now another liquid of density ρ1(ρ1<ρ2) is slowly poured in the container to a height h as shown. There is only denser liquid in the capillary tube. The rise of denser liquid in the capillary tube is also h. Assuming zero contact angle, the surface tension of heavier liquid is
View SolutionWater rises in a capillary tube through a height l. If the tube is inclined to the liquid surface at 30∘ the liquid will rise in the tube upto it's length equal to
View SolutionDue to capillary action, a liquid will rise in the capillary tube if the angle of contact is
View Solution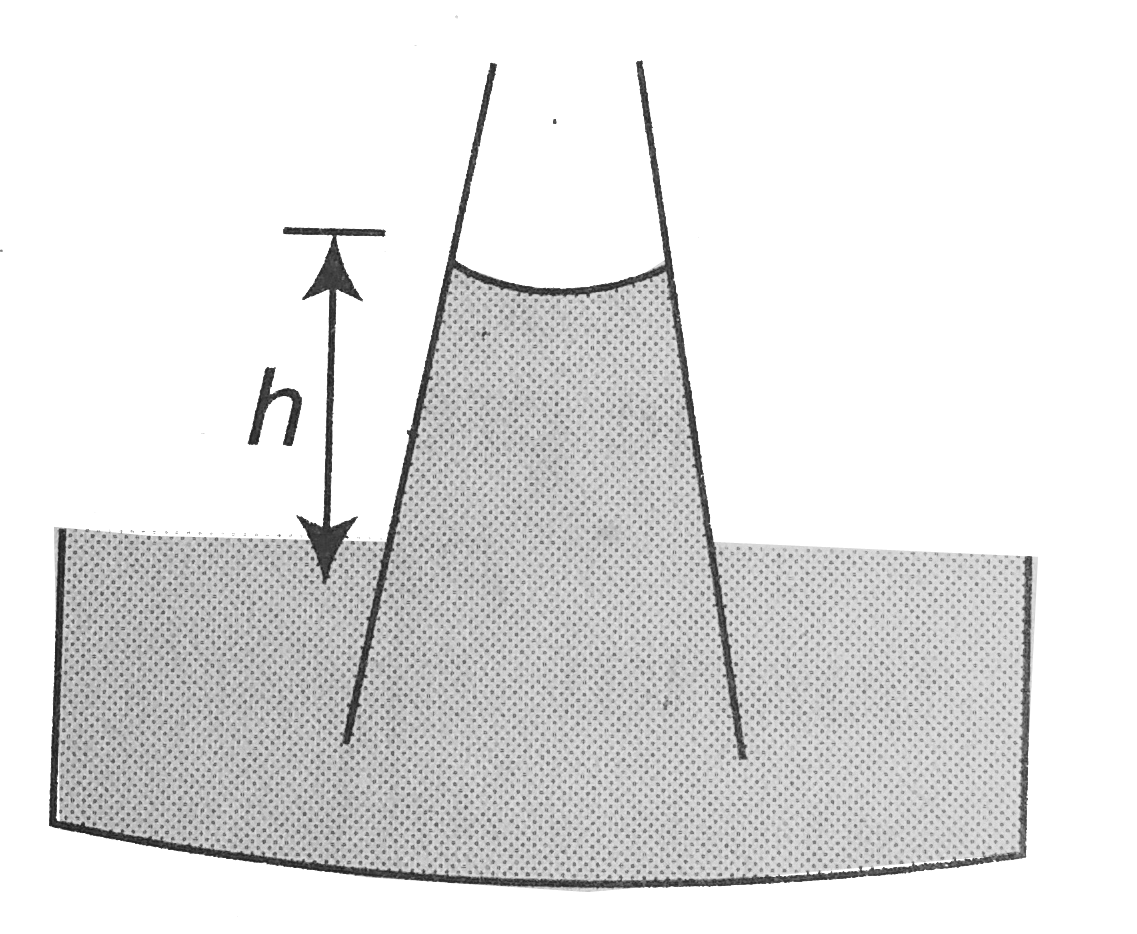
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View Solution
