What will be the nature of graph between the velocity of fluid flow (υ) and area of cross-section (a) of the pipe ?
To determine the nature of the graph between the velocity of fluid flow (ν) and the area of cross-section (A) of a pipe, we can follow these steps:
1. Understanding the Principle of Continuity:
- The principle of continuity states that for an incompressible fluid flowing through a pipe of varying cross-section, the mass flow rate must remain constant. This can be expressed mathematically as:
A1⋅V1=A2⋅V2
- Here, A1 and A2 are the areas of the cross-section at two different points in the pipe, and V1 and V2 are the corresponding velocities of the fluid at those points.
2. Rearranging the Equation:
- From the continuity equation, we can express the velocity in terms of the area:
V=CA
- where C is a constant (specifically, C=A⋅V). This shows that velocity is inversely proportional to the area of the cross-section.
3. Identifying the Relationship:
- Since we have established that V is inversely proportional to A, we can write:
V∝1A
4. Graphical Representation:
- To graph this relationship, we plot velocity (V) on the vertical axis and area (A) on the horizontal axis. The relationship V∝1A indicates that as the area increases, the velocity decreases.
- This results in a hyperbolic curve, specifically a rectangular hyperbola.
5. Conclusion:
- The nature of the graph between the velocity of fluid flow (ν) and the area of cross-section (A) of the pipe is a rectangular hyperbola. This indicates that with an increase in the area of the cross-section, the velocity of the fluid flow decreases.
Summary:
The graph of velocity (ν) versus area (A) is a rectangular hyperbola, demonstrating the inverse relationship between these two quantities.
---
- The principle of continuity states that for an incompressible fluid flowing through a pipe of varying cross-section, the mass flow rate must remain constant. This can be expressed mathematically as:
A1⋅V1=A2⋅V2
- Here, A1 and A2 are the areas of the cross-section at two different points in the pipe, and V1 and V2 are the corresponding velocities of the fluid at those points.
- From the continuity equation, we can express the velocity in terms of the area:
V=CA
- where C is a constant (specifically, C=A⋅V). This shows that velocity is inversely proportional to the area of the cross-section.
- Since we have established that V is inversely proportional to A, we can write:
V∝1A
- To graph this relationship, we plot velocity (V) on the vertical axis and area (A) on the horizontal axis. The relationship V∝1A indicates that as the area increases, the velocity decreases.
- This results in a hyperbolic curve, specifically a rectangular hyperbola.
- The nature of the graph between the velocity of fluid flow (ν) and the area of cross-section (A) of the pipe is a rectangular hyperbola. This indicates that with an increase in the area of the cross-section, the velocity of the fluid flow decreases.
The graph of velocity (ν) versus area (A) is a rectangular hyperbola, demonstrating the inverse relationship between these two quantities.
Topper's Solved these Questions
- Mechanical Properties of fluidsBook:SL ARORAChapter:Mechanical Properties of fluidsExercise:Exercise
Explore 459 Videos
- Mathematical toolsBook:SL ARORAChapter:Mathematical toolsExercise:Exercise
Explore 20 Videos
- Mechanical Properties of SolidsBook:SL ARORAChapter:Mechanical Properties of SolidsExercise:Example
Explore 113 Videos
Similar Questions
The resistance force arising due to pressure difference at the front and rear sides of a body in a fluid stream depends upon the density of the fluid, the velocity of flow and the maximum area of cross-section perpendicular to the flow. Show that the force varies as the square of the velocity.
View SolutionAyesha is watering the plants in her garden with a pipe of area of cross-section 'A' and observed that the force of water from the pipe is 'F'. Find the change in area of cross section of the pipe to attain a pressure difference which is 1.5 times that of the initial.
View Solution
Knowledge Check
A stone is lying in a fluid stream. The force acting on it depends on the density of the fluid, the velocity of flow and the maximum area of cross-section perpendicular to the direction of flow. The force F and the velocity v of flow are related as
AF∝1vBF∝vCF∝v2DF∝1v2If cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
 A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of these
A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of theseWhich of the following is the graph between the time and the velocity of a body moving in a viscous fluid?
A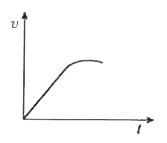 B
B C
C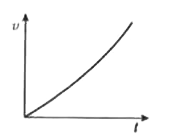 D
D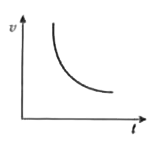
TheThe velocity of flow of water in the main water supply pipe is 1.0ms−1. What is the velocity in the deliverty pipe if area of cross-section of the supply pipe is 16 times that of the delivery pipe?
View SolutionA liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.

View SolutionA horizontal pipe of area of cross-section a and 3a respectively, then the ratio of velocity of flow at two different cross-section (If flow is streamline) is
View SolutionA liquid flows through a pipe of non-uniform cross-section. If A1andA2 are the cross-sectional areas of the pipe at two points, the ratio of velocities of the liquid at these points will be
View SolutionWater flows steadily through a horizontal pipe of a variable cross-section. If the pressure of water is p at a point where the velocity of flow is v, what is the pressure at another point where the velocity of flow is 2v, ρ being the density of water?
View Solution
