The temperature gradient in a rod 0.5 m long is per metre. The temperature of the hotter end is . What is the temperature of its colder end?
To solve the problem, we need to find the temperature of the colder end of the rod given the temperature gradient and the temperature of the hotter end. Here’s the step-by-step solution:
Step 1: Understand the Given Information
- Length of the rod (L) = 0.5 m
- Temperature gradient (dT/dx) = 40 °C/m
- Temperature of the hotter end (Th) = 30 °C
Step 2: Set Up the Relationship
The temperature gradient tells us how much the temperature changes per unit length. The change in temperature (ΔT) over a distance (Δx) can be expressed as:
ΔT=(Temperature gradient)×(Length)
Here, we want to find the temperature difference between the hotter end and the colder end:
Th−Tc=(dT/dx)×L
Step 3: Substitute the Known Values
Substituting the known values into the equation:
Th−Tc=40°C/m×0.5m
Calculating the right side:
Th−Tc=20°C
Step 4: Rearrange to Find Tc
Now, we can rearrange the equation to find the temperature of the colder end (Tc):
Tc=Th−20°C
Substituting the value of Th:
Tc=30°C−20°C
Step 5: Calculate Tc
Now, calculate Tc:
Tc=10°C
Final Answer
The temperature of the colder end of the rod is 10 °C.
---
- Length of the rod (L) = 0.5 m
- Temperature gradient (dT/dx) = 40 °C/m
- Temperature of the hotter end (Th) = 30 °C
The temperature gradient tells us how much the temperature changes per unit length. The change in temperature (ΔT) over a distance (Δx) can be expressed as:
ΔT=(Temperature gradient)×(Length)
Here, we want to find the temperature difference between the hotter end and the colder end:
Th−Tc=(dT/dx)×L
Substituting the known values into the equation:
Th−Tc=40°C/m×0.5m
Calculating the right side:
Th−Tc=20°C
Now, we can rearrange the equation to find the temperature of the colder end (Tc):
Tc=Th−20°C
Substituting the value of Th:
Tc=30°C−20°C
Now, calculate Tc:
Tc=10°C
The temperature of the colder end of the rod is 10 °C.
Topper's Solved these Questions
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- THERMODYNAMICSBOOK - SL ARORACHAPTER - THERMODYNAMICSEXERCISE - Exercise
342 Videos
Similar Questions
The temperature gradient in a rod of 1m long is '100^@' C/m if the temperature of hotter end is '30^@' C, then the temperature of colder end is
View SolutionTwo rods of same dimensions, but made of different materials are joined end to end to end with their free end being maintained at 100∘C and 0∘C respectively. The temperature of the junction is 70∘C. Then the temperature of the junction if the rods are inerchanged will be equal to T∘C Find T:
View Solution
Knowledge Check
The temperature gradient in a rod of 0.5 m long is 80∘C/m. If the temperature of hotter end of the rod is 30∘C, then the temperature of the colder end is
A40∘CB−10∘CC10∘CD0∘CThe temperature gradient in a rod of 0.5m length is 80∘C/m. It the temperature of hotter end of the rod is 30∘C, then the temperature of the cooler end is
A40∘CB−10∘CC10∘CD0∘CThe ends of a thin bar are maintained at different temperatures. The temperature of the cooler end is 11∘C , while the temperature at a point 0.13m from the cooler end is 23∘C and the temperature of the warmer end is 48∘C. Assuming that heat flows only along the length of the bar ( the sides are insulated), find the length of the bar.
A0.50mB0.40mC0.23mD0.64m
A Carnot cycle has an efficiency of 40% . Its low temperature resrvoir is at 7∘C . What is the temperature of source ?
View SolutionThe two rods show in figure have identical geomerical dimension.. They are in contact with two heat baths at temperature 100∘C . And 0∘C . The temperature of the junction is 70^(@)C . Find the temperature of the junction if the rods are interchanged.

View SolutionThe temperature of a body falls from 40∘C to 30∘C in 10 minutes. If the temperature of surrounding is 15∘C, then time to fall the temperature from 30∘C to 20∘C
View SolutionIn the figure-II temperature of inner surface of cylinder is 0∘C and temperature of outer surface is 100∘C. In figure-I temperature of one end of cylinder is 100∘Cwhile another end is at 0∘C
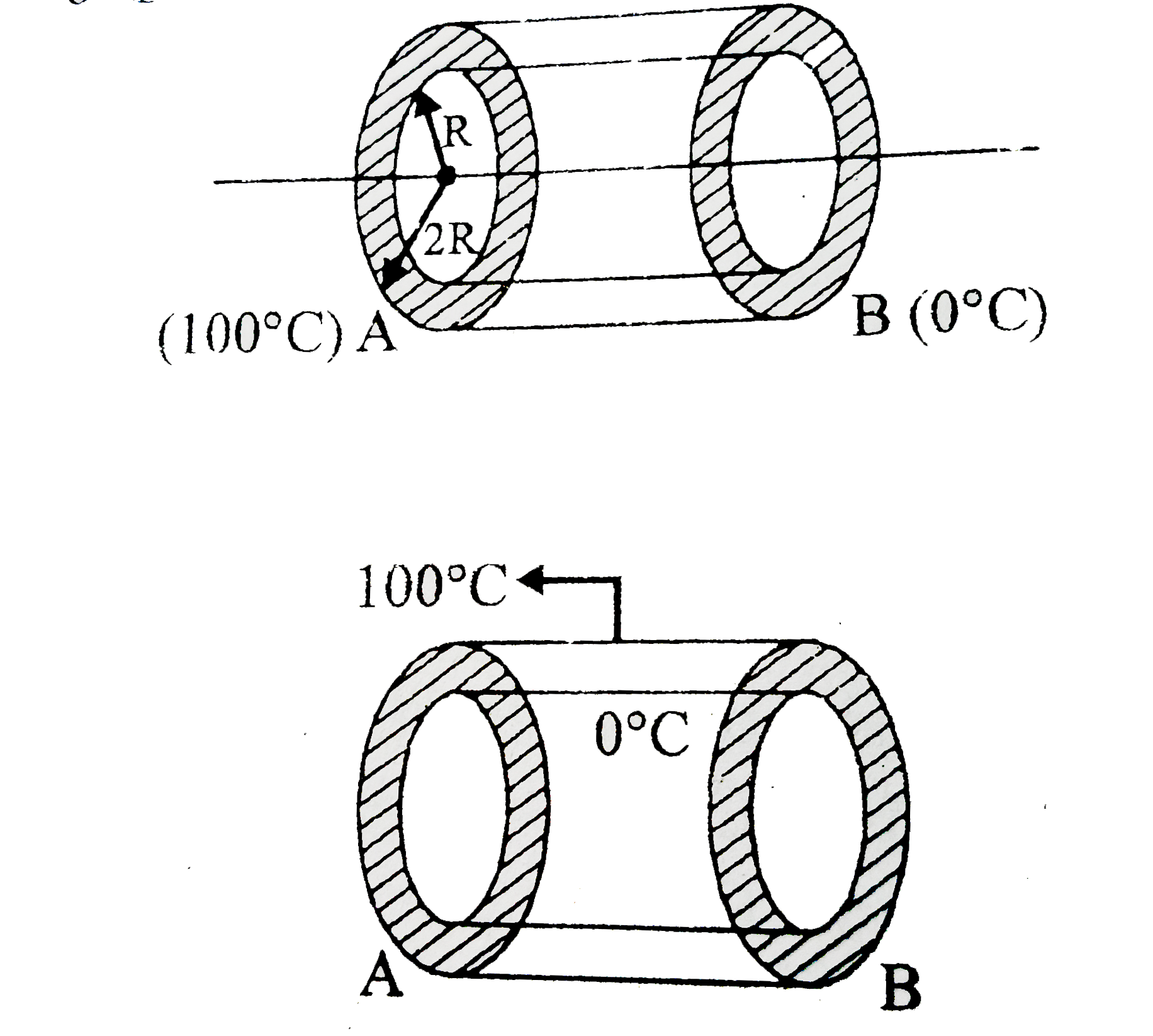
dTdr =temperature gradient in radial direction at steady state in figure -II
dTdl=temperature gradient in linear direction at steady state in figure -I . both cylinder are made of uniform material
View SolutionThe ratio of radiant energies radiated per unit surface area by two bodies is 16:1, the temperature of hotter body is 1000 K , then the temperature of colder body will be
View Solution
