One mole of an ideal gas undergoes a cyclic change ABCD where the (P,V) co-ordinates are A (5,1), B (5,3), C (2,3) and D (2,1). P is atmosphere and V is in litre. Calculate work done along AB, BC, CD and DA and also net work done in the process. Given 1atmosphere=1.01×105Nm−2.
To solve the problem of calculating the work done along the paths AB, BC, CD, and DA for one mole of an ideal gas undergoing a cyclic process, we will follow these steps:
Step 1: Identify the coordinates and convert pressure
The coordinates of the points are:
- A (5, 1)
- B (5, 3)
- C (2, 3)
- D (2, 1)
The pressure at point A (PA) is 5 atm. We need to convert this pressure into SI units (Pascals):
PA=5atm=5×1.01×105N/m2=5.05×105N/m2
Step 2: Calculate work done along AB
The work done (W) during an isobaric process (constant pressure) is given by:
W=PΔV
Where ΔV=VB−VA=3−1=2L. We need to convert liters to cubic meters:
ΔV=2L=2×10−3m3
Now, substituting the values:
WAB=PAΔV=(5.05×105)×(2×10−3)=1010J
Step 3: Calculate work done along BC
In the process BC, the volume remains constant (V = 3 L). Therefore, the work done is:
WBC=0J
Step 4: Calculate work done along CD
For the process CD, the pressure is constant at point C (PC = 2 atm):
PC=2atm=2×1.01×105N/m2=2.02×105N/m2
The change in volume is:
ΔV=VD−VC=1−3=−2L=−2×10−3m3
Now substituting the values:
WCD=PCΔV=(2.02×105)×(−2×10−3)=−404J
Step 5: Calculate work done along DA
In the process DA, the volume remains constant (V = 1 L). Therefore, the work done is:
WDA=0J
Step 6: Calculate net work done in the cycle
The net work done in the cyclic process is the sum of the work done in each segment:
Wnet=WAB+WBC+WCD+WDA
Substituting the values:
Wnet=1010+0−404+0=606J
Final Result
The net work done in the process is:
606J
The coordinates of the points are:
- A (5, 1)
- B (5, 3)
- C (2, 3)
- D (2, 1)
PA=5atm=5×1.01×105N/m2=5.05×105N/m2
The work done (W) during an isobaric process (constant pressure) is given by:
W=PΔV
Where ΔV=VB−VA=3−1=2L. We need to convert liters to cubic meters:
ΔV=2L=2×10−3m3
Now, substituting the values:
WAB=PAΔV=(5.05×105)×(2×10−3)=1010J
In the process BC, the volume remains constant (V = 3 L). Therefore, the work done is:
WBC=0J
For the process CD, the pressure is constant at point C (PC = 2 atm):
PC=2atm=2×1.01×105N/m2=2.02×105N/m2
The change in volume is:
ΔV=VD−VC=1−3=−2L=−2×10−3m3
Now substituting the values:
WCD=PCΔV=(2.02×105)×(−2×10−3)=−404J
In the process DA, the volume remains constant (V = 1 L). Therefore, the work done is:
WDA=0J
The net work done in the cyclic process is the sum of the work done in each segment:
Wnet=WAB+WBC+WCD+WDA
Substituting the values:
Wnet=1010+0−404+0=606J
The net work done in the process is:
606J
Topper's Solved these Questions
Similar Questions
One mole of an ideal gas undergoes a cyclic change ABCD where the (P-V) co-ordinates are A(5, 1), B(5, 3), C(2, 3) and D(2, 1). P is in atmosphere and V is in litre. Calculate work done along AB , BC, CD and DA and also net work done in the process. Given 1 atmosphere =1.01×105Nm−2.
View SolutionOne mole of an ideal gas undergoes a cyclic change ABCD where the (P,V) co-ordinates are A (5,1), B (5,3), C (2,3) and D (2,1). P is atmosphere and V is in litre. Calculate work done along AB, BC, CD and DA and also net work done in the process. Given 1atmosphere=1.01×105Nm−2.
View Solution
Knowledge Check
One mole of an ideal gas undergoes a cyclic process ABCDA as shown in the P-V diagram, The net work done in the process is
(1atm=106 dyne cm−2) A500 JB700 JC800 JD900 J
A500 JB700 JC800 JD900 JOne mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure . Temperature at point 1 =300K and process 2−3 is isothermal .
_S01_113_O01.png) .
.
Net work done by gas in complete cycle isA(9ln3+12)P0V0B(9ln3+4)P0V0C(9ln3−4)P0V0D(9ln3−8)P0V0Two moles of an ideal gas are undergone a cyclic process 1-2-3-1. If net heat exchange in the process is 300J, the work done by the gas in the process 2-3 is
 A−500JB−5000JC−3000JDNone of these
A−500JB−5000JC−3000JDNone of these
One mole of an ideal gas undergoes a cyclic change ABCD. From the given diagram calculate the net work done in the process.
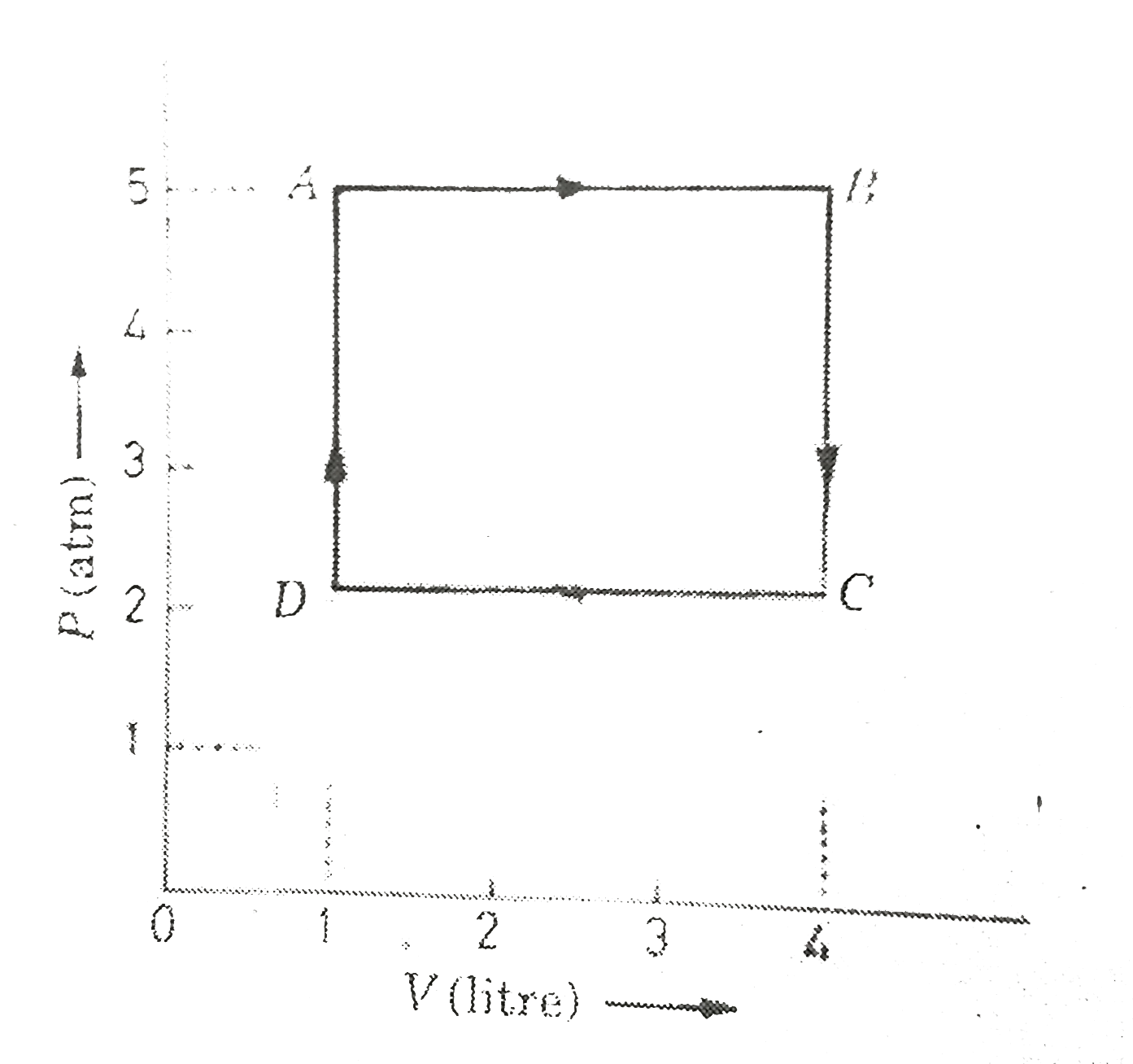
View SolutionOne mole of an ideal gas undergoes a cyclic change ABCDA as shown in (figure). What is the net work done (in joule) in the process? Take 1atm=105Pa.
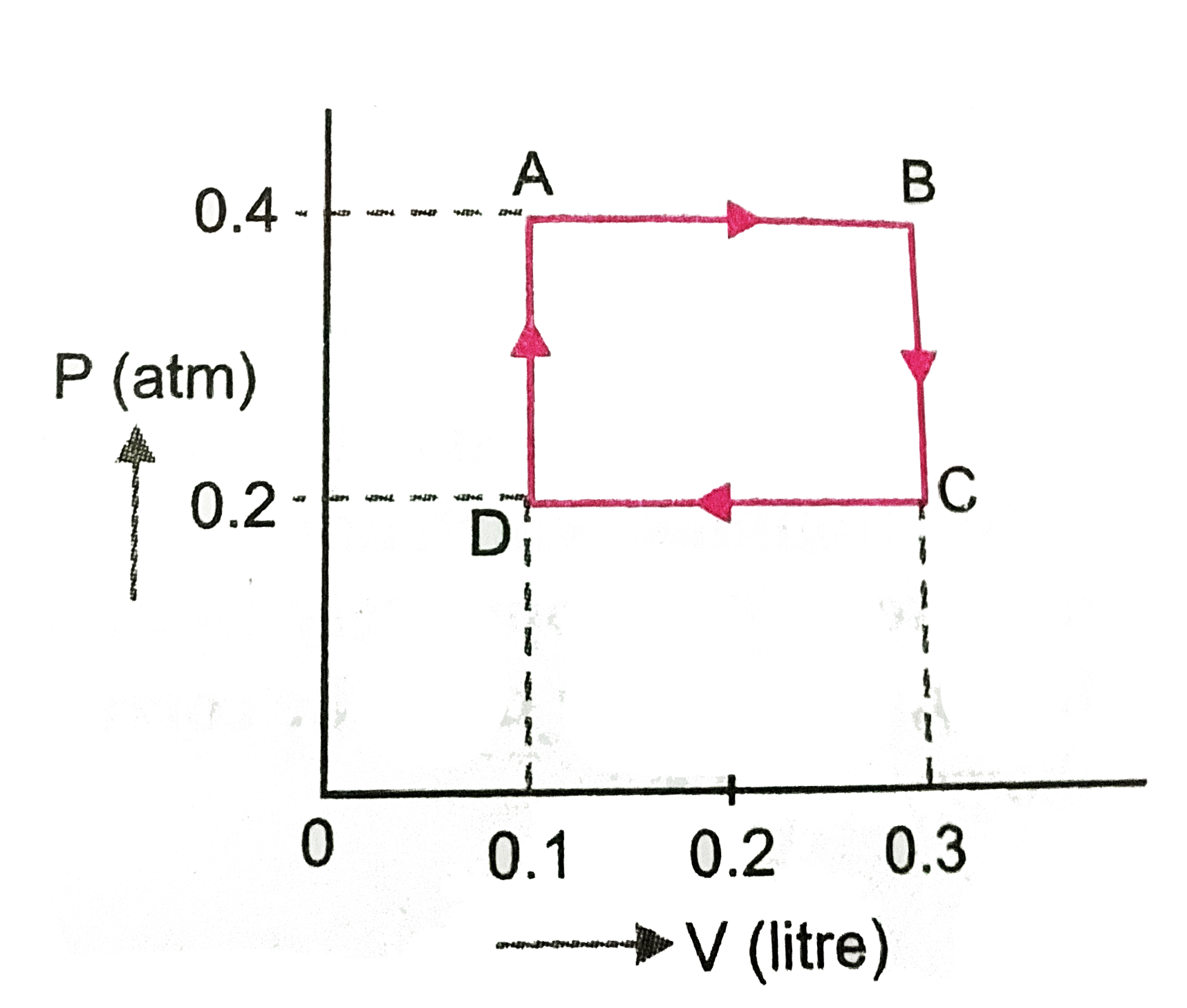
View SolutionAn ideal monoatomic gas is taken around the cycle ABCDA, wher co-ordinates of A, B, C and D on and D on P−V diagram are A(p,V),B(2p,V),C(2p,2V)andD(p,2V). Calculate work done during the cycle.
View SolutionABCD is rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). If P, Q, R and S be the midpoint of AB, BC, CD and DA respectively, show that PQRS is a rhombus.
View SolutionThe P−V diagram for a cyclic process is a triangle ABC drawn in order (figure). The co-ordinates of A,B,C are (4,1),(2,4)and(2,1) respectively. The co-ordinates are in the order (P,V) Pressure is in Nm−2 and volume is in liter. Calculate work done during the process from A to B, B to C and C to A. Also, calculate work done in the complete cycle.
View Solution
