A system goes from state A to B via two processes I and II, as shown in Fig. 12.25, How are $δ μ_{1}$ and $δ μ_{2}$ (the changes in internal energies in the processes I and II) related to each other ?

Video Solution

|

Answer

Step by step video & image solution for A system goes from state A to B via two processes I and II, as shown in Fig. 12.25, How are delta mu_1 and delta mu_2 (the changes in internal energies in the processes I and II) related to each other ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A system goes from A to B via two processes I and II as shown in the figure. If $Δ U_{1}$ and $Δ U_{2}$ are the changes in the internal energies in the processes I and II respectively, then -

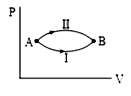A $Δ U_{1} = Δ U_{2}$
Brelation between $Δ U_{1} and Δ U_{2}$ cannot be determined
C $Δ U_{2} > Δ U_{1}$
D $Δ U_{2} < Δ U_{1}$
Question 2 - Select One
A system goes from A and B via two processes. I and II as shown in figure. If $Δ U_{1} and Δ U_{2}$ are the changes in internal enregies in the processes I and II respectively, then

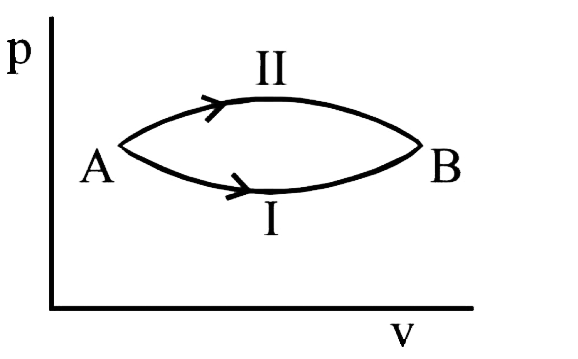Arelation between $Δ U_{1}$ and $Δ u_{2}$ can not be determined
B $Δ U_{1} = Δ U_{2}$
C $Δ U_{2} < Δ U_{1}$
D $Δ U_{2} > Δ U_{1}$
Question 3 - Select One
Let $Δ U_{1}$ and $Δ U_{2}$ be the changes in internal energy of an ideal gas in the processes $A$ and $B$ then
A $Δ U_{1} > Δ U_{2}$
B $Δ U_{1} = Δ U_{2}$
C $Δ U_{1} < Δ U_{2}$
D $Δ U_{1} \neq Δ U_{2}$

SL ARORA-FLUIDS AT REST-Problem for self practice

Home
Ask Doubt
Profile