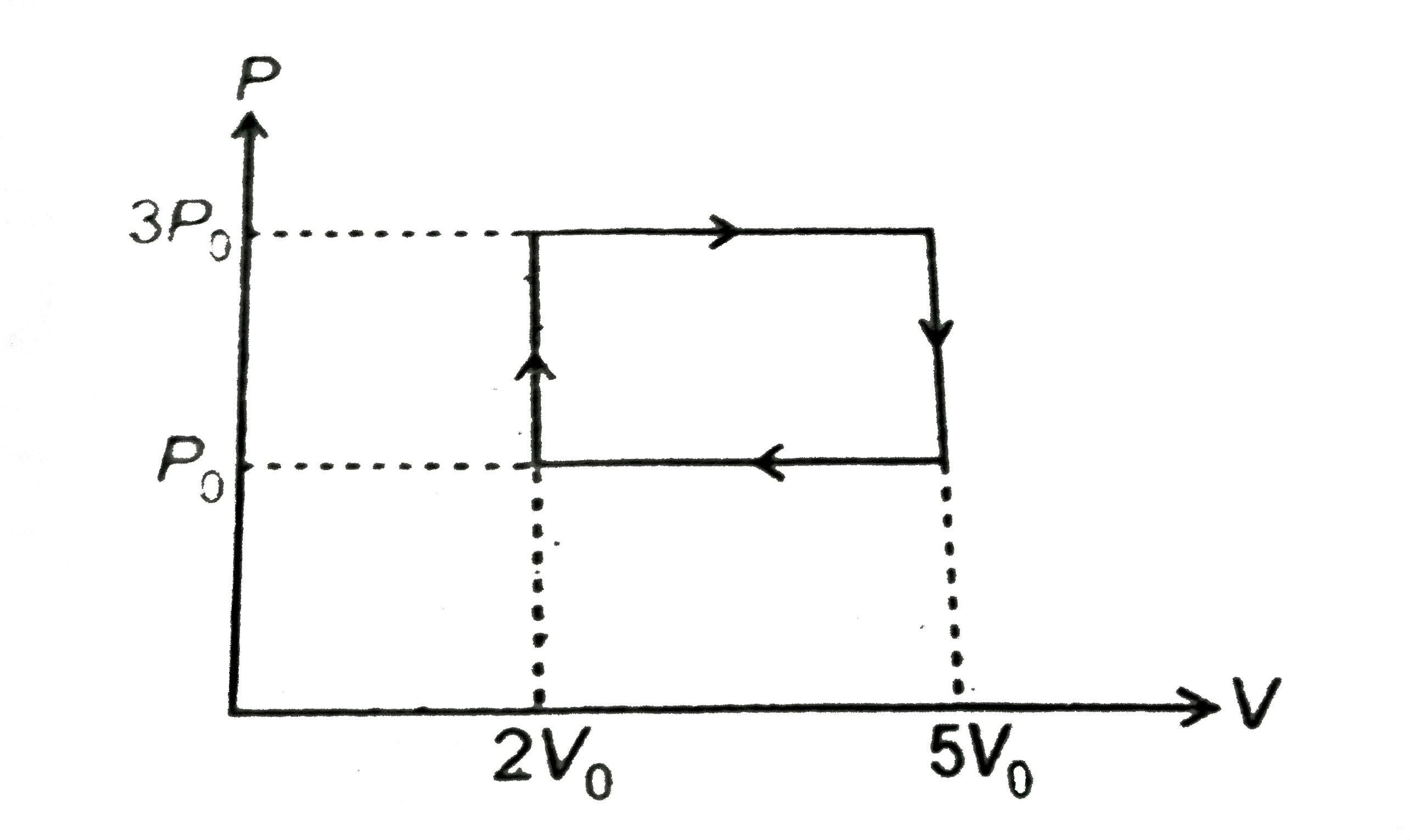
What is a cyclic process ? Prove that the net work done during a cyclic process is numerically equal to the area of the loop representing the cycle.
Step-by-Step Solution
1. Definition of a Cyclic Process:
- A cyclic process is a thermodynamic process in which a system undergoes a series of transformations and returns to its initial state. This means that the initial state and final state of the system are the same.
2. Representation in a PV Diagram:
- To visualize this process, we can use a Pressure-Volume (PV) diagram. In this diagram, the x-axis represents volume (V) and the y-axis represents pressure (P). The cyclic process will form a closed loop on this diagram.
3. Identifying the States:
- Let’s denote the states in the cyclic process as A, B, C, and back to A. The process moves from A to B, then from B to C, and finally from C back to A.
4. Work Done in a PV Diagram:
- The work done by the system during a thermodynamic process can be calculated using the formula:
W=∫PdV
- This integral represents the area under the curve in the PV diagram.
5. Work Done from A to B:
- From state A to state B, the volume increases (expansion). Therefore, the work done (W_AB) is positive and is equal to the area under the curve from A to B.
6. Work Done from B to C:
- From state B to state C, the volume decreases (compression). Thus, the work done (W_BC) is negative, and it is equal to the area under the curve from B to C, but taken as negative.
7. Work Done from C to A:
- From state C back to state A, the volume again decreases. The work done (W_CA) is also negative and is equal to the area under the curve from C to A, taken as negative.
8. Calculating Net Work Done:
- The net work done during the entire cyclic process can be expressed as:
Wnet=WAB+WBC+WCA
- Substituting the areas:
Wnet=Area under A to B−Area under B to C−Area under C to A
9. Final Area Calculation:
- The net work done is equal to the area enclosed by the loop in the PV diagram. This area represents the total work done by the system during one complete cycle.
10. Conclusion:
- Therefore, we have proved that the net work done during a cyclic process is numerically equal to the area of the loop representing the cycle in the PV diagram.
- A cyclic process is a thermodynamic process in which a system undergoes a series of transformations and returns to its initial state. This means that the initial state and final state of the system are the same.
- To visualize this process, we can use a Pressure-Volume (PV) diagram. In this diagram, the x-axis represents volume (V) and the y-axis represents pressure (P). The cyclic process will form a closed loop on this diagram.
- Let’s denote the states in the cyclic process as A, B, C, and back to A. The process moves from A to B, then from B to C, and finally from C back to A.
- The work done by the system during a thermodynamic process can be calculated using the formula:
W=∫PdV
- This integral represents the area under the curve in the PV diagram.
- From state A to state B, the volume increases (expansion). Therefore, the work done (W_AB) is positive and is equal to the area under the curve from A to B.
- From state B to state C, the volume decreases (compression). Thus, the work done (W_BC) is negative, and it is equal to the area under the curve from B to C, but taken as negative.
- From state C back to state A, the volume again decreases. The work done (W_CA) is also negative and is equal to the area under the curve from C to A, taken as negative.
- The net work done during the entire cyclic process can be expressed as:
Wnet=WAB+WBC+WCA
- Substituting the areas:
Wnet=Area under A to B−Area under B to C−Area under C to A
- The net work done is equal to the area enclosed by the loop in the PV diagram. This area represents the total work done by the system during one complete cycle.
- Therefore, we have proved that the net work done during a cyclic process is numerically equal to the area of the loop representing the cycle in the PV diagram.
Topper's Solved these Questions
Similar Questions
Knowledge Check
For a cyclic process
AW = 0BΔE=0CΔH≠0DΔE≠0What is true for a cyclic process
AW=0BΔE=0CΔH=0DΔE≠0A cyclic process is shown in the figure. Work done during the cyclic process ABCDA is
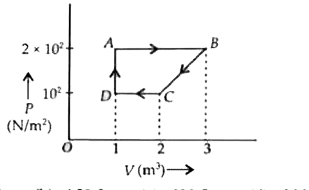 A160 JB150 JC600 JD900 J
A160 JB150 JC600 JD900 J
Can the work done during a cyclic process be zero?
View SolutionWork Done In Cyclic Process
View SolutionA cyclic process is shown in the figure. Work done during the cyclic process ABCDA is
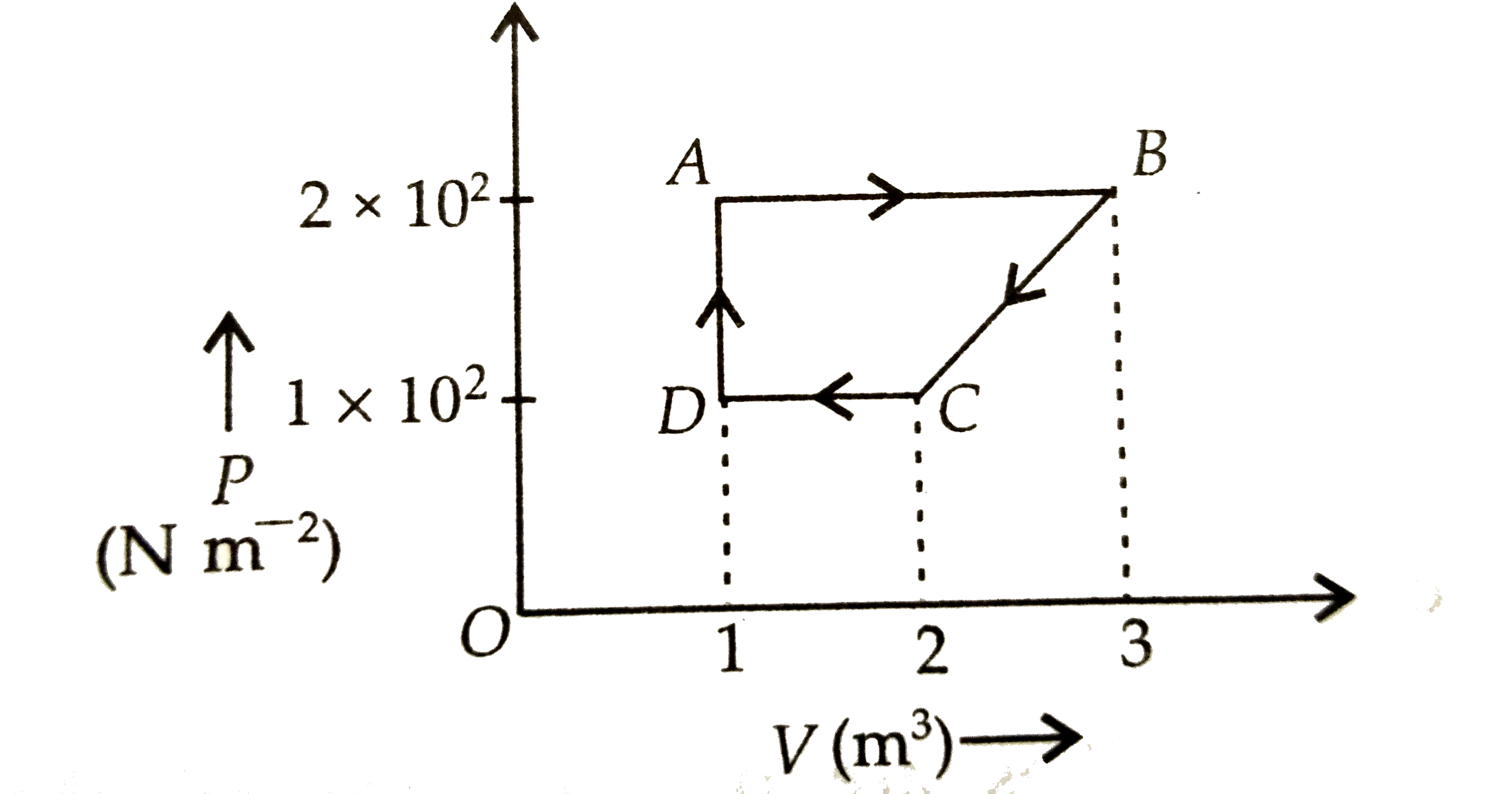
View SolutionA cyclic process is shown in the figure. Work done during the cyclic process ABCDA is

View SolutionThe work obtained in cyclic process is zero because
View Solution