Determine the numerical values of R and kB
To determine the numerical values of the universal gas constant R and the Boltzmann constant kB, we can follow these steps:
Step 1: Determine the value of R
1. Identify the conditions: We will use the ideal gas law, which states that PV=nRT. We will consider 1 mole of an ideal gas at Standard Temperature and Pressure (STP).
- Standard Temperature (T) = 273 K
- Standard Pressure (P) = 1 atm
2. Convert pressure to SI units:
- 1 atm = 0.76 m of Hg
- To convert this to Pascals (N/m²), we use the density of mercury (ρHg=13.6×103kg/m3) and gravitational acceleration (g=9.8m/s2):
P=0.76m×13.6×103kg/m3×9.8m/s2
3. Calculate the volume at STP: The molar volume of an ideal gas at STP is approximately 22.4L=22.4×10−3m3.
4. Substitute values into the ideal gas equation:
R=PVnT
Substituting n=1mol, T=273K, and the calculated pressure P and volume V:
R=(0.76×13.6×103×9.8)×(22.4×10−3)1×273
5. Calculate R: After performing the calculations, we find:
R≈8.31J/(mol K)
Step 2: Determine the value of kB
1. Use the relationship between R and kB:
kB=RNA
where NA (Avogadro's number) is approximately 6.022×1023mol−1.
2. Substitute the values:
kB=8.31J/(mol K)6.022×1023mol−1
3. Calculate kB:
kB≈1.38×10−23J/K
Final Results:
- The value of R is 8.31J/(mol K).
- The value of kB is 1.38×10−23J/K.
- Standard Temperature (T) = 273 K
- Standard Pressure (P) = 1 atm
- 1 atm = 0.76 m of Hg
- To convert this to Pascals (N/m²), we use the density of mercury (ρHg=13.6×103kg/m3) and gravitational acceleration (g=9.8m/s2):
P=0.76m×13.6×103kg/m3×9.8m/s2
R=PVnT
Substituting n=1mol, T=273K, and the calculated pressure P and volume V:
R=(0.76×13.6×103×9.8)×(22.4×10−3)1×273
R≈8.31J/(mol K)
kB=RNA
where NA (Avogadro's number) is approximately 6.022×1023mol−1.
kB=8.31J/(mol K)6.022×1023mol−1
kB≈1.38×10−23J/K
- The value of R is 8.31J/(mol K).
- The value of kB is 1.38×10−23J/K.
Topper's Solved these Questions
Similar Questions
Knowledge Check
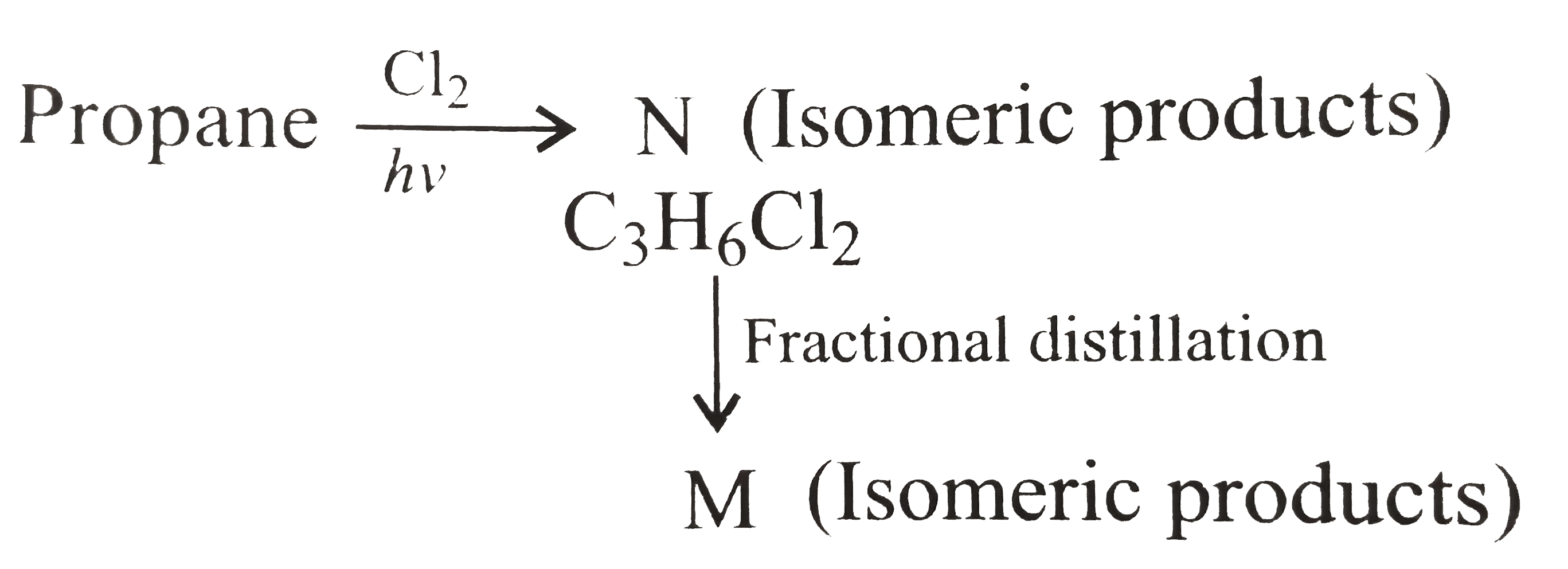
What are the numerical values of N and M?A6,6B5,4C4,4D3,3If the quadratic equation x2+ax+b=0andx2+bx+a=0(a≠b) have a common root, the find the numeical value of a +b.
A1B-1C0D2If the quadratic equation x2+ax+b=0andx2+bx+a=0(a≠b) have a common root, the find the numeical value of a +b.
A1B0C-1Dnone of these
If A+B=π4, find the numerical value of (1+tan A)(1+tan B) is equal to
View SolutionIf A=[i−i−ii] B=[1−1−11] and ifA2=αB,α inR⋅ then the numerical value of α32is
View SolutionIn the equaiton PV=nRT, which one cannot be the numerical value of R
View SolutionIf (a2+b2)3=(a3+b3)2 and ab≠0 then the numerical value of ab+ba is equal to-
View SolutionThe area and perimeter of a square are numerically equal, then the numerical value of the side of the square is
View Solution
