A harmonic wave travelling in a medium has a period T and wavelength X. How are X and T related ?
To find the relationship between the wavelength (λ) and the period (T) of a harmonic wave traveling in a medium, we can follow these steps:
1. Understand the Definitions:
- Wavelength (λ): The distance between two consecutive points that are in phase on a wave (e.g., crest to crest or trough to trough).
- Period (T): The time taken for one complete cycle of the wave to pass a given point.
2. Wave Speed Formula:
- The speed (v) of a wave is defined as the distance traveled per unit time. Thus, we can express this relationship as:
v=DistanceTime=λT
- Here, λ is the wavelength and T is the period.
3. Rearranging the Formula:
- From the wave speed formula, we can rearrange it to express the relationship between wavelength and period:
λ=v⋅T
- This shows that the wavelength is equal to the wave speed multiplied by the period.
4. Substituting Variables:
- In the context of the question, if we denote the wavelength as X instead of λ, we can write:
X=v⋅T
- This indicates that the wavelength (X) is directly proportional to the period (T), given a constant wave speed (v).
5. Conclusion:
- Therefore, the relationship between the wavelength (X) and the period (T) of the wave can be summarized as:
X∝T(for constant wave speed)
- Wavelength (λ): The distance between two consecutive points that are in phase on a wave (e.g., crest to crest or trough to trough).
- Period (T): The time taken for one complete cycle of the wave to pass a given point.
- The speed (v) of a wave is defined as the distance traveled per unit time. Thus, we can express this relationship as:
v=DistanceTime=λT
- Here, λ is the wavelength and T is the period.
- From the wave speed formula, we can rearrange it to express the relationship between wavelength and period:
λ=v⋅T
- This shows that the wavelength is equal to the wave speed multiplied by the period.
- In the context of the question, if we denote the wavelength as X instead of λ, we can write:
X=v⋅T
- This indicates that the wavelength (X) is directly proportional to the period (T), given a constant wave speed (v).
- Therefore, the relationship between the wavelength (X) and the period (T) of the wave can be summarized as:
X∝T(for constant wave speed)
Similar Questions
A harmonic wave travelling in a medium has a period T and wavelength X. How far does the wave travel in time T ?
View SolutionA harmonic wave is travelling in a stationary medium whose equation of this wave w.r.t. a frame which is moving along -ve x-axis with a constant speed v w.r.t. stationary medium. Also, find speed of wave in moving frame.
View Solution
Knowledge Check
A harmonic wave is travelling along +ve x-axis, on a stretched string. If wavelength of the wave gets doubled, then
Afrequency of wave may changeBwave speed may changeCboth frequency and speed of wave may changeDonly frequency will changeThe equation of a simple harmonic progressive wave having amplitude 5 mm, period 2 second and wavelength 2m and travelling along the positive direction of the x-axis is given by
Ay=5sin2π(t2−x2)By=5×10−3sin2π(2t−x2)Cy=5×10−3sin2π(t2−x2)Dy=5×10−3sinπ(2t−x)
A sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
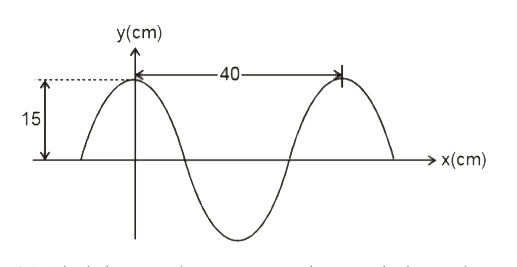
(a) Find the angular wave number, period angular frquency and speed of the wave.
View SolutionA sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
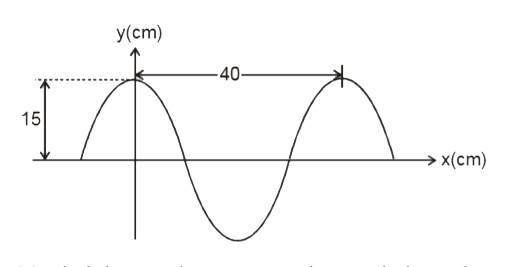
(b) Determine the phase constant ϕ, and write a general expression for the wave function.
View SolutionA wave represented by the given equationY=Asin(10πx+15πt+π3) , where x is in meter and t is in second. The expression represents
(1) A wave travelling in the negative X direction with a velocity of 1.5 m/sec
(2) A wave travelling in the negative X direction with a wavelength of 0.2 m
(3) A wave travelling in the positive X direction with a velocity of 1.5 m/sec.
(4) A wave travelling in the positive X direction with a wavelength of 0.2 m
View SolutionA simple harmonic wave having an amplitude a and time period T is represented by the equation y = 5sinπ(t+4)m. Then the value of amplitude (a) in (m) and time period (T) in second are
View SolutionA sound wave is travelling in a medium.If equation of displacement wave in the medium is given by y = 2cos( 2πx −100πt + π2 ) then equation of pressure waves will be (B → Bulk modulus of medium)
(А) P= 4Bπ sin(2πx− 100πt)
(В) P= 4Bπ sin(2πx+ 100πt)
(C) P= 4Bπ cos(2πx− 100πt)
(D) P= 4Bπ cos(2πx+ 100πt)
View SolutionA sinusoidal wave travelling in the positive x direction has an amplitude of 15cm, wavelength 40cm and freqency 8Hz. The vertical displacement of the medium at t=0 and x=0 os also 15cm, as shown.
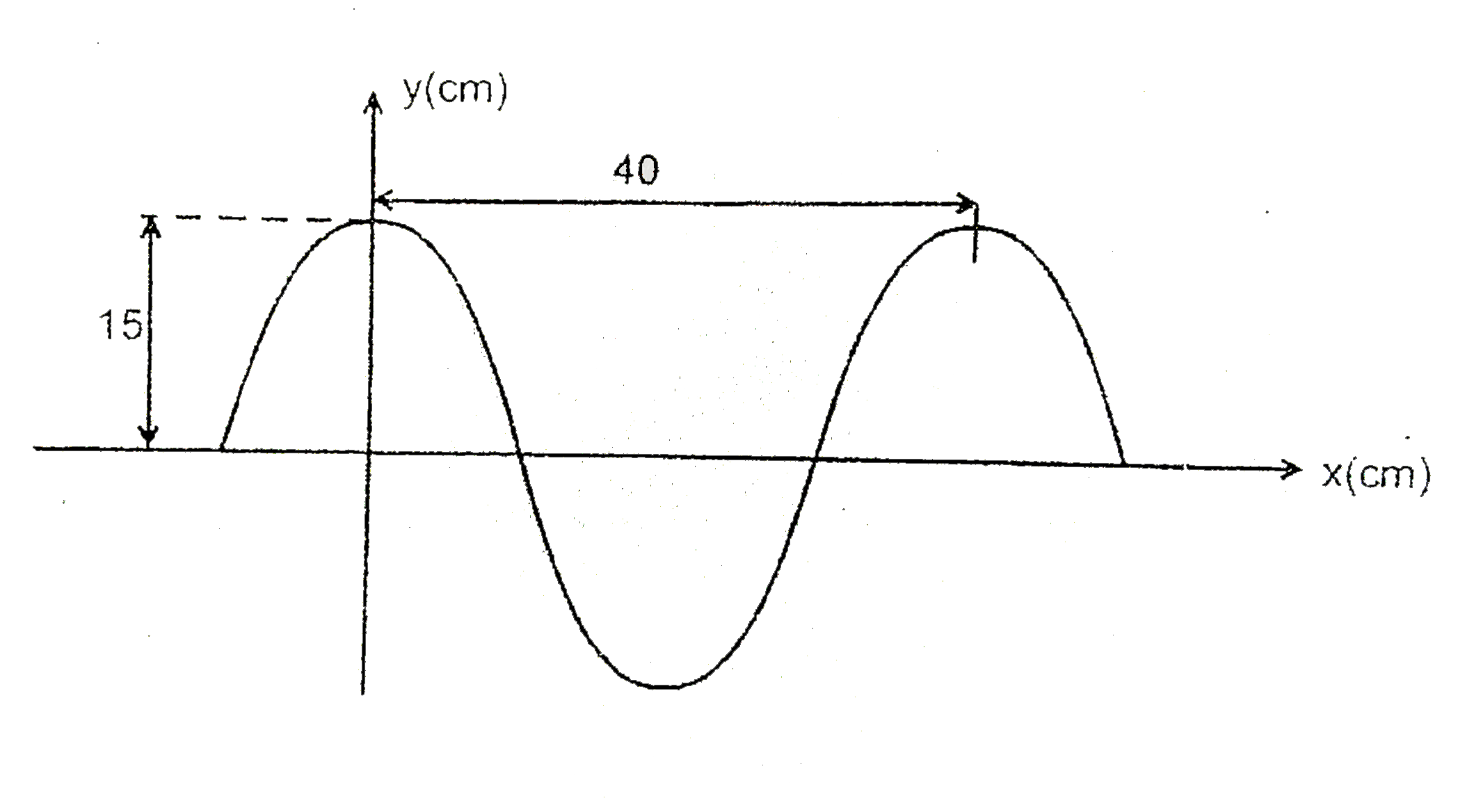
(a) Find the angular wave number, period, angualr frequency and speed of the wave.
(b) Datermine the phase constant ϕ, and write a general expression for the two wave function.
View Solution
