Derive an expression for the nth mode of vibration in case of a closed end organ pipe. Hence give the value of v1:v2:v3.
To derive the expression for the nth mode of vibration in a closed-end organ pipe, we need to understand the behavior of standing waves in such a pipe. A closed-end organ pipe has one end closed and the other end open, resulting in specific boundary conditions for the standing waves.
1. Understanding the Closed-End Pipe:
- In a closed-end organ pipe, the closed end is a displacement node (minimum displacement), and the open end is a displacement antinode (maximum displacement).
- The fundamental frequency (first mode) will have a quarter of a wavelength fitting into the length of the pipe.
2. Fundamental Mode (n=1):
- For the first mode (n=1), the length L of the pipe is given by:
L=λ14
- Rearranging gives:
λ1=4L
3. Higher Modes (n=2, 3, ...):
- For the nth mode, the length of the pipe corresponds to:
L=(2n−1)λn4
- Rearranging gives:
λn=4L2n−1
4. Finding the Frequencies:
- The speed of sound in the pipe is given by v. The frequency fn for the nth mode is related to the wavelength by:
fn=vλn
- Substituting λn:
fn=v4L2n−1=(2n−1)v4L
5. Finding the Ratios of Frequencies:
- The frequencies for the first three modes are:
- For n=1:
f1=1⋅v4L
- For n=2:
f2=3v4L
- For n=3:
f3=5v4L
- The ratio of frequencies f1:f2:f3 is:
f1:f2:f3=1:3:5
Final Expression:
The expression for the nth mode of vibration in a closed-end organ pipe is:
λn=4L2n−1
And the ratio of frequencies for the first three modes is:
f1:f2:f3=1:3:5
- In a closed-end organ pipe, the closed end is a displacement node (minimum displacement), and the open end is a displacement antinode (maximum displacement).
- The fundamental frequency (first mode) will have a quarter of a wavelength fitting into the length of the pipe.
- For the first mode (n=1), the length L of the pipe is given by:
L=λ14
- Rearranging gives:
λ1=4L
- For the nth mode, the length of the pipe corresponds to:
L=(2n−1)λn4
- Rearranging gives:
λn=4L2n−1
- The speed of sound in the pipe is given by v. The frequency fn for the nth mode is related to the wavelength by:
fn=vλn
- Substituting λn:
fn=v4L2n−1=(2n−1)v4L
- The frequencies for the first three modes are:
- For n=1:
f1=1⋅v4L
- For n=2:
f2=3v4L
- For n=3:
f3=5v4L
- The ratio of frequencies f1:f2:f3 is:
f1:f2:f3=1:3:5
The expression for the nth mode of vibration in a closed-end organ pipe is:
λn=4L2n−1
And the ratio of frequencies for the first three modes is:
f1:f2:f3=1:3:5
Similar Questions
Diagrammatically show first two modes of vibrations in case of an open organ pipe and write the ratio of their frequencies
View SolutionAn open organ pipe has fundamental frequency 300Hz.The first overtone of the open organ pipe is the same as the first overtone of a closed organ pipe. The length of the closed organ pipe is (v_(sound)=330m/s) (A) 10cm (B) 41cm (C) 82cm (D) 164cm
View Solution
Knowledge Check
In the case of closed end organ pipe
Athe maximum possible wavelength is same as that of open end organ pipeBthe maximum possible wavelength is less than that of open end organ pipeCthe maximum possible wavelength may be less than that of open end organ pipeDthe maximum possible wavelength is greater than that of open end organ pipeModes of vibration in a closed organ pipe are represented by –
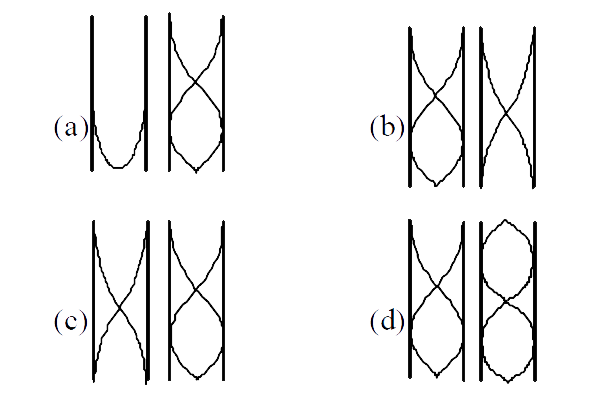 AaBbCcDd
AaBbCcDdIf the end correction of closed organ pipe is 0.3 cm then the diameter of the tube will be
A0.05mB0.5mC1cmD3cm
Discuss different modes of vibrations in an air column of a pipe open at both the ends. State the cause of end correction. Find the end correction for the pipe open at both the ends in fundamental mode.
What should be tension applied to a wire of length 1m and maas 10 g, if it has to vibrate with fundamental frequency of 50 Hz?
View Solution(a) What is kinetic energy due to ? Derive an expression for it in case of a body of mass m moving with velocity v.
(b) If W is the work done to give a speed v to a car from rest, how much work is done to increase its speed to 2v ?
View SolutionIn the case of vibration of closed end organ pipe in fundamental mode of vibratin, the pressure id maximum at
View SolutionTwo vibrating string of same length, same cross section area and stretched to same tension is made of materials with densities ρ and 2ρ. Each string is fixed at both ends If v0 represents the fundamental mode of vibration of the one made with density ρ and v2 for another Then v1/v2 is:
View SolutionAssertion: An open organ pipe of certain length has the same fundamental frequency as closed organ pipe of half the length.
Reason : In case of an open organ organ pipe, at both the ends antinodes are formed while in case of closed organ pipe, at one end antinode and at the other end node is formed.
View Solution
