Write down Bbohr.s model of hydrogen atom. Solution in Gujrati
(i) Principal quantum number : The stationary states for electron are numbered n = 1,2,3 These integral number are know as principal quantum numbers.
(ii) Stationary orbit radili (r ) : The radil of the stationary states are expressed as :
rn=n2a0
where a0=52.9±
The radius of the first stationary (n-1) state called the Bohr.s orbit is 52.9 pm
Normally the elecrron in the hydrogen atom is found in this orbit (that is n=1)
(iii) energy of stationary state : The most important property associated with the electron is the energy of its stationary state it is given by the expression.
When the electron is free the influence of nucleus the energy is taken as zero . The electron in this situation is associated with the stationary state of principal Quantum number = in this situation electron is free from H atom and become (H+) hydrogen ion.
When the electron is attracted by the nucleus and its energy is lowered . That is the reason for the presence of negative sigh in equation and depicts its stability relative to the reference state of zero energy and n= so Energy of electrons in atom is less than the free electron.
E∝=0
(iv) boh.s theory for isoelectronic ion of hydrogen
Bohr.s theory can also applied to the ions containing only one electron similar to that present in hydrogen atom.
The energies of the stationary states known as hydrogen like species ) are given by the expression.
En=−2.18×10−18.z2n21
Where z= atomic number =2,3,4 for the helium lithium beryllium respectively
From the above equations it is evident that the value of energy becomes more negative and that of radius becomes smaller with increase of Z
(v ) Velocity of electron
It is also possible to calculate teh velocities of electrons moving in these orbits ,
Although the precise equation is not given here qualitatively the magnitude of velocity positive charge on the nucleus and decreases with increase of principal quantum number
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - STRUCTURE OF ATOMEXERCISE - Section -A (Try Your Self -1)4videos
STRUCTURE OF ATOM
- BOOK - KUMAR PRAKASHANCHAPTER - STRUCTURE OF ATOMEXERCISE - Section -A (Try Your Self -2)5videos
STRUCTURE OF ATOM
- BOOK - KUMAR PRAKASHANCHAPTER - STATES OF MATTER EXERCISE - QUESTION PAPER FROM MODULE (SECTION - A)4videos
STATES OF MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - THE P-BLOCK ELEMENTSEXERCISE - SECTION-D NCERT EXEMPLAR SOLUTION (MCQs) LONG ANSWER25videos
THE P-BLOCK ELEMENTS
Similar Questions
Find neutron electron and proton in the following
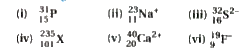
05:14View SolutionCalculate the number of electron in one mole N−3 ion.
01:59View SolutionGiven Dalton.s Law of partial Pressure, its mathematical formula and explain aqueous tension.
02:54View SolutionDescribe the general trends in the following properties of the elements in Groups-13
Atomic size04:39View Solutionरदरफोर्ड परमाणु मॉडल के दोष लिखिए।
02:54View SolutionWriter Bohr's postulates for the hydrogen atom model.
04:39View SolutionWrite down the postulates of Bohr atom model.
02:54View SolutionWrite down the draw backs of Bohr atom model.
04:39View SolutionWrite down the postulates of Bohr atom model.
01:59View SolutionWrite down the draw backs of Bohr atom model.
02:33View SolutionWrite down the postulates of Bohr atom model.
06:04View SolutionWrite down the draw backs of Bohr atom model.
02:35View SolutionWriter Bohr's postulates for the hydrogen atom model.
02:22View SolutionExplain Rutherford nuclear model of atom
02:35View SolutionWrite postulates of Bohr.s model of hydrogen atom
04:22View Solution