The electron energy in hydrogen atom is given by Calculate the energy required to remove an electron completely from the n=2 orbit .What is the longest wavelength of ligth in cm that can be used to cause this transitiion ? Solution in Gujrati
Energy requried to remove electron
and
Calculation of longest wavelength for to
The longest wavelength of this transition means least energy
So wavelength of to transition
Topper's Solved these Questions
- STRUCTURE OF ATOMBook:KUMAR PRAKASHANChapter:STRUCTURE OF ATOMExercise:Section -A (Try Your Self -1)
Explore 4 Videos
- STRUCTURE OF ATOMBook:KUMAR PRAKASHANChapter:STRUCTURE OF ATOMExercise:Section -A (Try Your Self -2)
Explore 5 Videos
- STATES OF MATTER Book:KUMAR PRAKASHANChapter:STATES OF MATTER Exercise:QUESTION PAPER FROM MODULE (SECTION - A)
Explore 4 Videos
- THE P-BLOCK ELEMENTSBook:KUMAR PRAKASHANChapter:THE P-BLOCK ELEMENTSExercise:SECTION-D NCERT EXEMPLAR SOLUTION (MCQs) LONG ANSWER
Explore 25 Videos
Similar Questions
Find neutron electron and proton in the following
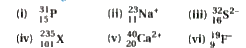
View SolutionCalculate the number of electron in one mole N−3 ion.
View SolutionGiven Dalton.s Law of partial Pressure, its mathematical formula and explain aqueous tension.
View SolutionDescribe the general trends in the following properties of the elements in Groups-13
Atomic size
View SolutionThe electron energy in hydrogen atom is given by E_(n) = (-21.7 xx 10^(-12)/(n^(2))) erg Calculate the energy required to remove an electron completely from the n = 2 .What is the longest wavelength (in cm) of light can be used to cases this transition ?
View SolutionThe electron energy in hydrogen atom is given by E_(n)=(-2.18xx10^(-8))//n^(2)J . Calculate the energy required to remove an electron completely from the n=2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
View Solutionहाइड्रोजन परमाणु में इलेक्ट्रॉन की ऊर्जा En=(−2.18×10−18)/n2J द्वारा दी जाती है। n=2 कक्षा से इलेक्ट्रॉन को पूरी तरह निकालने के लिए आवश्यक ऊर्जा की गणना कीजिए। प्रकाश की सबसे लम्बी तरंग-दैर्ध्य (cmमें) क्या होगी, जिसका उपयोग इस संक्रमण में किया जा सके।
View SolutionThe electron energy in hydrogen atom is given by E_(n)=(-2.18xx10^(-18))//n^(2)J . Calculate the energy required to remove the electron completely from n=2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition ?
View Solutionहाइड्रोजन परमाणु में इलेक्ट्रॉन की ऊर्जा En=(−2.18×10−18)/n2 द्वारा दी जाती है । n=2 कक्षा से इलेक्ट्रॉन को पूरी तरह निकालने के लिए आवश्यक ऊर्जा की गणना कीजिए। प्रकाश की सबसे लम्बी तरंग-दैध्य्र ( cm में ) क्या होगी जिसका उपयोग इस संक्रमण में किया जा सके ?
View Solutionहाइड्रोजन परमाणु में इलेक्ट्रॉन की ऊर्जा निम्न प्रकार व्यक्त की जाती है-
En=(−21.7×10−12)n2अर्ग
n=2 कक्ष से एक इलेक्ट्रॉन को पूर्णतया पृथक करने के लिए आवश्यक ऊर्जा की गणना कीजिए । इस संक्रमण के लिए प्रकाश की दीर्घतम (longest) तरंगदैध्र्य की क्या होगी ?
View Solutionहाइड्रोजन परमाणु के इलेक्ट्रॉन की ऊर्जा En=(−2.18×10−18/n2)J द्वारा दी जाती हैं। n=2 कक्षा से इलेक्ट्रॉन को पूरी तरह निकालने के लिए आवश्यक ऊर्जा की गणना कीजिए । प्रकाश की सबसे लम्बी तरंगदैध्र्य ( cm में) क्या होगी, जिसका उपयोग इस संक्रमण में किया जा सके?
View SolutionThe electron energy is hydrogen atom is given by E(n)=(−2.18×10−18)J. Calculate the energy required to remove an electron completely from the n=2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
View Solutionहाइड्रोजन परमाणु में इलेक्ट्रॉन की ऊर्जा E=2.17×10−12n2 अर्ग है। n=2 वाली कक्षा से एक इलेक्ट्रॉन को पूर्ण रूप से निष्कासित करने के लिए आवश्यक ऊर्जा की गणना कीजिए। इस संक्रमण के लिए प्रयोग होने वाले प्रकाश की दीर्घतम तरंग-दैर्घ्य (सेमी में) कितना होगा?
View SolutionThe electron energy in hydrogen atom is given ny E_n=(-2.18xx10^(-18))/(n^(2))J .Calculate the energy required to remove an electron completely from the n=2 orbit.What is the longest wavelength of light in cum that can be used to cause this transition?
View SolutionCalculate the energy required to remove an electron completely from n = 2 orbit. What is the longest wave length of light that can be used to cause this transition?
View Solution
