Explain compressibility factor (Z). Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

Compressibility factor (Z) : Deviation between real gas and idea gas is known as compressibility factor (Z).
$Z = \frac{p V}{n R T}$ …..(Eq. -i)
where, Z = 1
Z = Compressibility factor of ideal gas deviation behaviour,
$Z = \frac{V_{real}}{V_{ideal}} = \frac{real molar volume}{ideal molar volume}$ .......(constant T)
For $Z = 1, Z > 1, Z < 1$ is give in points (i), (ii), (iii)
(i) Z = 1 OR 1 deviation factor :
For ideal gas Z = 1 at all temperature and pressure , because pV = nRT.
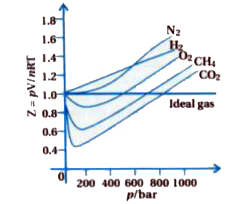
If Z = 1 then gas is ideal gas and $Z \to p$ graph is parallel line.
At very low pressures all gases shown have Z = 1 and behave as an ideal gas.
Ideal gas law, follow at Z = 1 at Boyle temperature of Boyle point at real pressure.
(ii) $Z > 1$ OR Positive deviation :
At high pressure all real gases shows $Z > 1$ they are less compressible than ideal gas. If $Z > 1$ than permanently gas.
$N_{2}, H_{2} O_{2}$ shows positive deviation, $Z \to p$ graph show positive deviation.
According to diagram for $H_{2}$ gas at high pressure $Z > 1$ . When pressure increases value of Z becomes more positive.
Ideal gas shows positive deviation of higher than Boyle.s point and value of a are higher than are then intermolecular attraction force are weak.
(iii) $Z < 1$ OR negative deviation :
At intermediate pressure, most gasses have $Z < 1$ .
For $O_{2}, C H_{4}, C O_{2}$ gas shows negative deviation, $Z \to p$ graph shows negative deviation.
According to diagram, $Z < 1$ at lower pressure. Initially pressure increases than Z decreases, after that z cross ideal gas line.
At lower temperature then Boyle.s point value of Z decreases at increases pressure, which reacted at minimum value and pressure is continuously increases.
(iv) Graph between $Z \to p$ for some gases :

(v) Relation between Z real gas and ideal molar volume :
$Z = \frac{p V_{real}}{n R T}$ .....(Eq. -i)
If gas is an ideal,
$V_{real} = \frac{n R T}{p}$ ......(Eq. -iii)
Value of $\frac{n R T}{p}$ is put in (iv) then we get equation (iii).
$Z = \frac{V_{real}}{V_{ideal}}$ ....(Eq. -v)
$∴ Z = \frac{Real molar volume}{Ideal molar volume}$ ......(constant T)
..Compressibility factor is ratio of real molar volume and ideal molar volume...

Updated on:21/07/2023

|

Class 11 CHEMISTRY STATES OF MATTER

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-STATES OF MATTER -QUESTION PAPER FROM MODULE (SECTION - A)

Home
Ask Doubt
Profile