Acceleration time graph of a particle is shown. Workdone by all the force acting on the particle of mass m in time interval t1 and t2, while a1 and a2 is the acceleration at time t1 and t2. Then find the value of a1 is ma21m21[t42−t41]. Then the value of n is
![Acceleration time graph of a particle is shown. Workdone by all the force acting on the particle of mass m in time interval t(1) and t(2), while a(1) and a(2) is the acceleration at time t(1) and t(2). Then find the value of a(1) is (ma(1)^(2))/(m(1)^(2))[t(2)^(4)-t(1)^(4)]. Then the value of n is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/AKS_TRG_AO_PHY_XI_V01_A_C08_E01_014_Q01.png)
Topper's Solved these Questions
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - LECTURE SHEET (EXERCISE-II KINETIC ENERGY, WORK ENERGY THEOREM STRAIGHT OBJECTIVE TYPE QUESTION)
14 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - LECTURE SHEET (EXERCISE -III CONSERVATIVE AND NON CONSERVATIVE FORCES STRAIGHT OBJECTIVE TYPE QUESTIONS)
13 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - LECTURE SHEET (EXERCISE-I WORKDONE BY FORCE LINKED COMPREHENSION TYPE QUESTIONS)
2 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
The displacement x of a particle along a straight line at time t is given by x=a0+a1t+a2t2. The acceleration of the particle is
View SolutionA body travels along a straight line with uniform acceleration a1 for time t1 and with uniform acceleration a2 for time t2 for time t2. What is the average acceleration?
View Solution
Knowledge Check
Acceleration time graph of a particle is shown work done by all the force acting on the particle of mass m in line internalt1 and t2 while a1 is the acceleration at time t1 given by t=0 particle was at rest
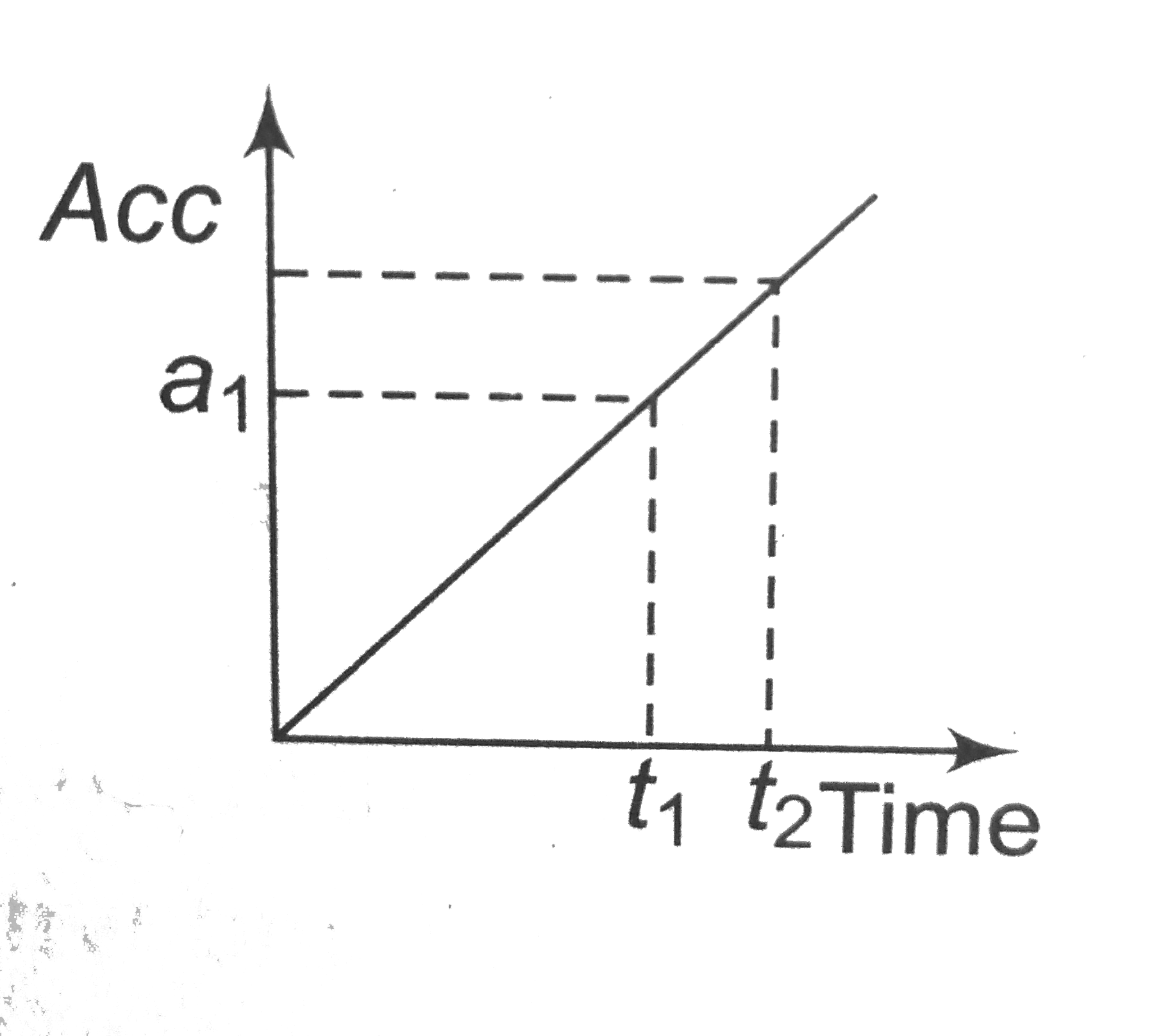 Ama214t1(t32−t21)Bma218t21(t42−t41)Cma214t21(t42−t41)Dma14t1(t22−t21)
Ama214t1(t32−t21)Bma218t21(t42−t41)Cma214t21(t42−t41)Dma14t1(t22−t21)A particle moves a distance x in time t according to equation x2=1+t2 . The acceleration of the particle is
A1x3B1x−1x2C−tx2D1x−t2x3The displacement x of a particle along a straight line at time t is given by x=a0−a1t+a2t2 . The acceleration of the particle is -
Aa0Ba1C2a2Da2
The displacement x of a particle along a straight line at time t is given by x=a0+a1t+a2t2. The acceleration of the particle is
View SolutionA scooter accelerates from rest for time t1 at constant rate a1 and then retards at constant rate a2 for time t2 and comes to rest. The correct value of t1t2 will be :-
View SolutionThe displacement 'x' of a particle moving along a straight line at time t is given by x=a0+a1t+a2t2. The acceleration of the particle is :-
View SolutionThe displacement x of a particle along a straight line at time t is given by : x=a0+a1t2+a23t2. The acceleration of the particle is
View SolutionThe activity of a sample of radioactive material A1 at time t1 and A2 at time t2(t2>t1). Its mean life is T.
View Solution
