In a conservation force field, a particle of mass 1 kg moving from rest from the origin. The potential energy at various x-coordinates as shown in graph. Find the correct option if dudy=dudz=0
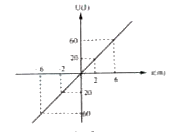
When the particle crosses -4m, the speed of the particle is 2√10m/sec
When the particle crosses -4m, the speed of the particle is 2√20 m/sec
The particle is moving along +x-axis.
The particle is moving along -x-axis.
The correct Answer is:A, B, D
Topper's Solved these Questions
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - LECTURE SHEET (EXERCISE -III CONSERVATIVE AND NON CONSERVATIVE FORCES INTEGER TYPE QUESTIONS)
1 Video
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - LECTURE SHEET (EXERCISE-IV POTENTIAL ENERGY STRAIGHT OBJECTIVE TYPE QUESTIONS)
8 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - LECTURE SHEET (EXERCISE-II KINETIC ENERGY, WORK ENERGY THEOREM STRAIGHT OBJECTIVE TYPE QUESTION)
14 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
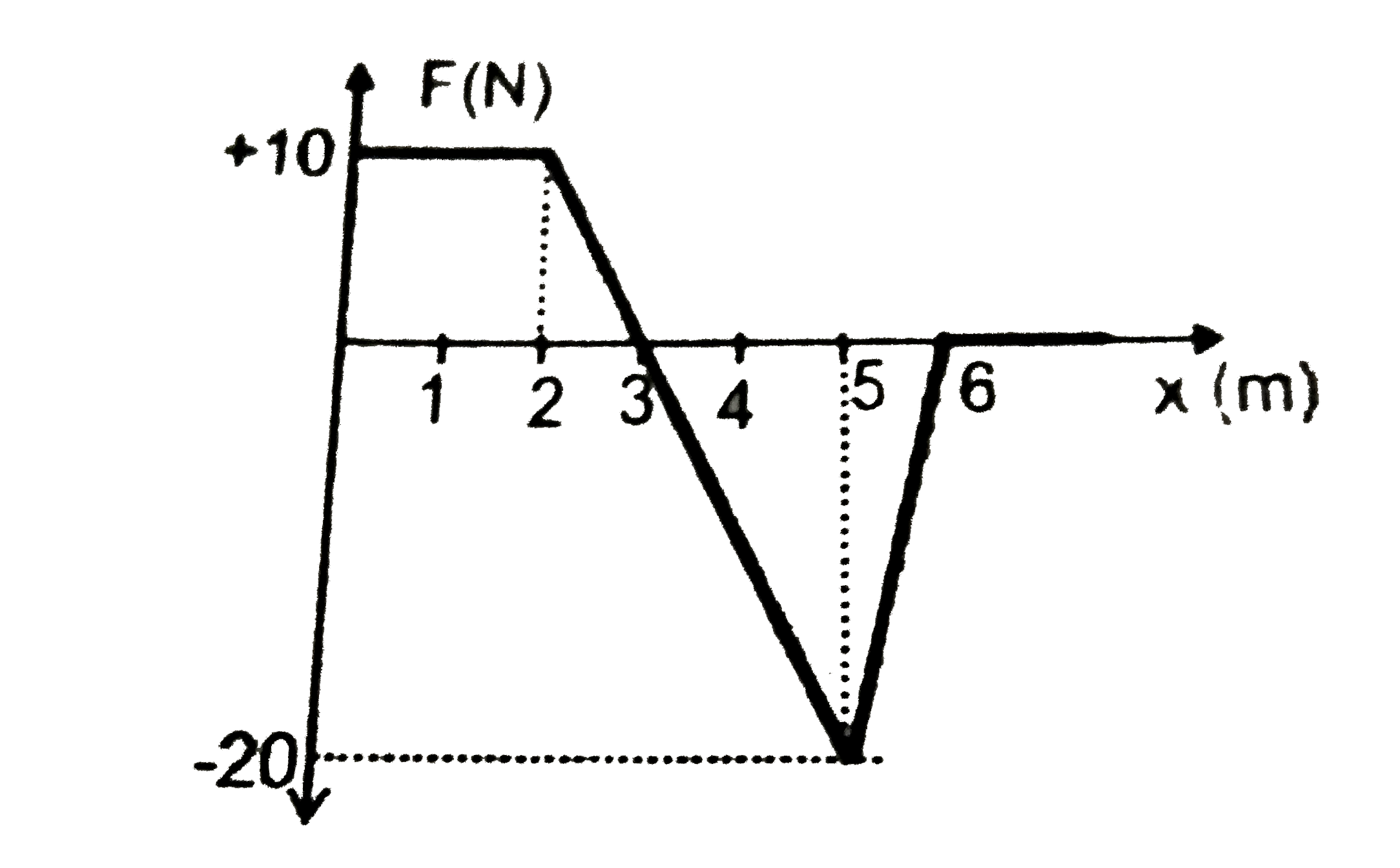
A particle of mass 1kg moves from rest along a straight line due to acition of a force F which varies with the displacement x as shown in graph−( Use 1√2=0.8 if needed )
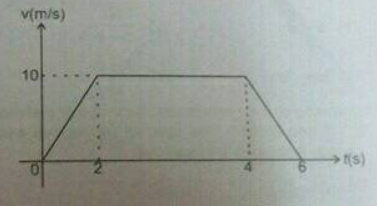
View SolutionA particle of mass 1 kg is moved under the action of a force and velocity time graph of the particle is shown in figure.Work done by the force from t=0 to t=6 s Is
View Solution
Knowledge Check
A particle of mass 1kg moves from rest along a straight line due to acition of a force F which varies with the displacement x as shown in graph−( Use 1√2=0.8 if needed )
 Amaximum K.E. of particle is 25JBTotal work done by froce on particle up to x=6m is −5JCThere will beno power delivered by the particle at x=3,5.3 and 6mDNone of these
Amaximum K.E. of particle is 25JBTotal work done by froce on particle up to x=6m is −5JCThere will beno power delivered by the particle at x=3,5.3 and 6mDNone of theseThe variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
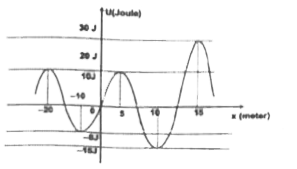 AIf the particle is released at the origin, then it will move towards x-axis.BAt x=10 particle is in unstable equilibriumCIf the particle is released at x=5+Δx, where Δx→0(Δx>0) then its maximum speed is √10m/sec.DAt x= 15m, the particle is in stable equilibrium.
AIf the particle is released at the origin, then it will move towards x-axis.BAt x=10 particle is in unstable equilibriumCIf the particle is released at x=5+Δx, where Δx→0(Δx>0) then its maximum speed is √10m/sec.DAt x= 15m, the particle is in stable equilibrium.A particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.
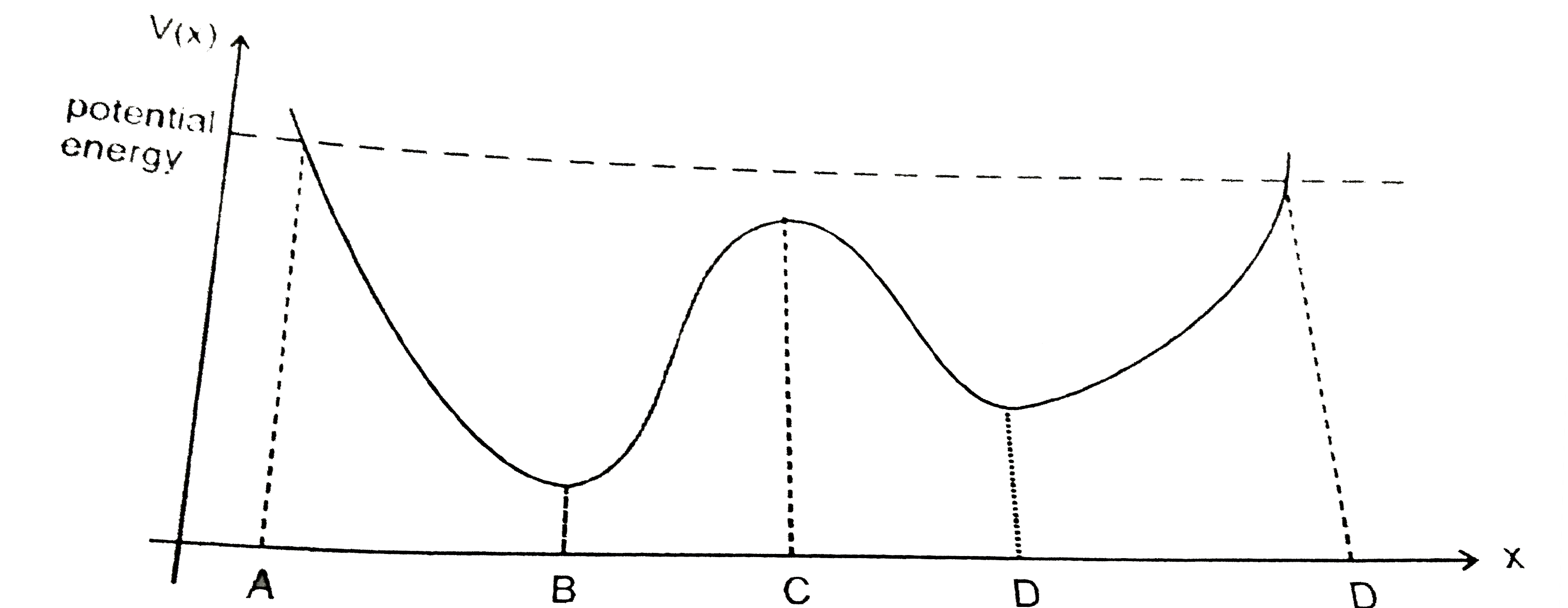
If the particle starts to move from rest from the point A, thenAthe speed is zero at the point A and E.Bthe acceleration vanished at the point A,B,D,C,ECthe acceleration vanished at the points B,C,DDthe speed is maximum at the point D.
The variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.

View SolutionThe gravitational field in a certain region is given as
→E=(3Nkg−1)ˆi+(5Nkg−1)ˆj
(a) What will be magnitude of gravitational force acting on a particle of mass 3 g which is placed at the origin ?
(b) What will be gravitational potential at point (12m, 0) and (0, 6m) considering that potential at origin is zero ?
(c ) A particle of mass 3 kg is moved from the origin to the point (9m, 4m). Calculate the change of gravitational potential energy.
(d) If the above particle is moved from (5m, 0) to (0, 5m), then find the change in potential energy.
View SolutionThe gravitational field in a region is given by →E=(5Nkg−1)→i+(12Nkg−1)→j.. a. find the magnitude of the gravitational force acting on a particle of mass 2 kg placed at the origin b. Find the potential at the points (12m,0) and (0,5m) if the potential at the origin is taken to be zero. c. Find the change in gravitational potential energy if a particle of mass 2 kg is taken from the origin to the point (12m,5m). d. Find the change in potential energy if the particle is taken from (12m,0) to (0,5m).
View SolutionThe gravitationasl fiedl in a region is given by →E=(5Nkg−1)→i+(12nk−1)→j.. a.find the magnitude of the gravitational force acting on a particle of mass 2 kg th gravittional fore actiing on a particle of mass 2 kg placed at the origin. B. Find the potential at teh points (12m,0) and (o,5m) if the potential at teh origin is taken to be zero. C. Find the change in gravitationa potential energyif a particle of mass 2 kg is taken from the origin to teh point (12m,5m). d. Find the change in potential energy if the particle is taken from (12m,0) to (0,5,m).
View SolutionA particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.

If the particle starts to move from rest from the point A, then
View Solution
