Find the average velocity of motion specified by the formula s=(t2−5t+2) m from t1=5sec to t2 =15 sec.
To find the average velocity of the motion specified by the formula s=t2−5t+2 from t1=5 seconds to t2=15 seconds, we can follow these steps:
Step 1: Understand the formula for average velocity
The average velocity Vavg over a time interval from t1 to t2 is given by the formula:
Vavg=s(t2)−s(t1)t2−t1
where s(t) is the displacement function.
Step 2: Calculate s(t1) and s(t2)
First, we need to calculate the displacement at t1=5 seconds and t2=15 seconds.
1. Calculate s(t1):
s(5)=(52)−5(5)+2=25−25+2=2 m
2. Calculate s(t2):
s(15)=(152)−5(15)+2=225−75+2=152 m
Step 3: Substitute values into the average velocity formula
Now we can substitute s(t1) and s(t2) into the average velocity formula:
Vavg=s(15)−s(5)15−5=152−215−5
Step 4: Simplify the expression
Now we simplify the expression:
Vavg=15010=15 m/s
Final Answer
The average velocity of the motion from t1=5 seconds to t2=15 seconds is 15 m/s.
---
The average velocity Vavg over a time interval from t1 to t2 is given by the formula:
Vavg=s(t2)−s(t1)t2−t1
where s(t) is the displacement function.
First, we need to calculate the displacement at t1=5 seconds and t2=15 seconds.
s(5)=(52)−5(5)+2=25−25+2=2 m
s(15)=(152)−5(15)+2=225−75+2=152 m
Now we can substitute s(t1) and s(t2) into the average velocity formula:
Vavg=s(15)−s(5)15−5=152−215−5
Now we simplify the expression:
Vavg=15010=15 m/s
The average velocity of the motion from t1=5 seconds to t2=15 seconds is 15 m/s.
Topper's Solved these Questions
- DIFFERENTIATION OF FUNCTIONS BOOK - IA MARONCHAPTER - DIFFERENTIATION OF FUNCTIONS EXERCISE - 2.2 (DIFFERENTIATION OF EXPLICIT FUNCTIONS)
7 Videos
- DIFFERENTIATION OF FUNCTIONS BOOK - IA MARONCHAPTER - DIFFERENTIATION OF FUNCTIONS EXERCISE - 2.3 (SUCCESSIVE DIFFERENTIATION OF EXPLICIT FUNCTION , LEIBNITZ FORMULA )
2 Videos
- BASIC CLASSES OF INTEGRABLE FUNCTIONS BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS
5 Videos
- IMPROPER INTEGRALSBOOK - IA MARONCHAPTER - IMPROPER INTEGRALSEXERCISE - 8.4 ADDITIONAL PROBLEMS
1 Videos
Similar Questions
Knowledge Check
The angle θ through which a pulley turns with time t is specified by the functionθ=t2+3t−5. Find the angular velocity ω=dθdt at t=5sec.
A15Rad/secB23Rad/secC13Rad/secD11Rad/secFind the distance travelled by a body having velocity v=1−t2 from t = 0 tol t = 2 sec .
A3mB2mC1mD4mCharge through a cross-section of a conductor is given by Q =5t2−2t coulomb. Find the average current through the conductor in the interval t1, = 2 s to t2= 4 s.
A14AB28AC56AD7A
If velocity of a particle is given by v=3t2−6t+4. Find its displacement from t=0 to 3secs.
View SolutionFind the modulus of average acceleration (in m/s2) of the block from time t = 2 sec to t = 4 sec.
View SolutionThe velocity time graph of a body moving in a straight line is shown. Find its
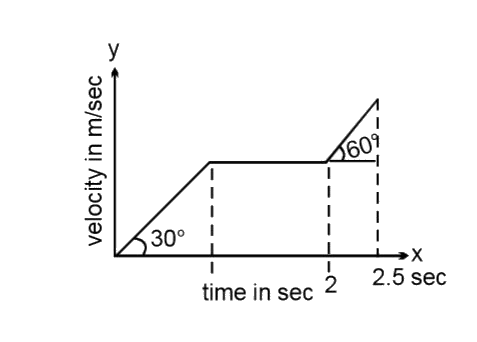
(a) instantaneous velocity at t = 1.5 sec (b) average acceleration from t = 1.5 sec. to t = 2.5 sec (c) draw its acceleration time graph from t = 0 to t = 2.5 sec
View SolutionThe instantaneous position of a moving drone is given by y=m+nt2, where m=6m and n=3.2 ms−2 and t is time. Find the velocity, the average velocity of drone between t=0 sec and 4 sec. also calculate the velocity at t=3sec.
View SolutionCharge through a cross section of a conductor is give by Q=5t2−2t coulomb .Find the average current through the conduction the interval t1=2s to t2=4s .
View Solution