A floor is paved with rectangular marble blocks, each of length a and breadth b. A circular block of diameter c(c<a,b) is thrown on the floor at random. Show that the chance that it falls entirely on one rectangular block is (a−c)(b−c)ab.
To solve the problem, we need to find the probability that a circular block of diameter c falls entirely on one rectangular block of dimensions a (length) and b (breadth).
1. Understanding the Problem:
- We have a rectangular block of dimensions a and b.
- A circular block of diameter c is thrown randomly onto the floor.
- We need to ensure that the entire circular block falls within the rectangular block.
2. Determine the Radius of the Circle:
- The radius R of the circular block is given by:
R=c2
3. Conditions for the Circle to Fall Entirely on the Rectangle:
- For the circular block to fall entirely on the rectangular block, the center of the circular block must be at least R (which is c2) away from the edges of the rectangular block.
- This means that the center of the circle must fall within a smaller rectangle formed inside the original rectangle.
4. Dimensions of the Smaller Rectangle:
- The effective length of the smaller rectangle where the center of the circle can fall is:
a−c
- The effective breadth of the smaller rectangle is:
b−c
5. Area of the Smaller Rectangle:
- The area of the smaller rectangle where the center of the circle can fall is:
Areasmall=(a−c)(b−c)
6. Area of the Original Rectangle:
- The area of the original rectangular block is:
Arealarge=ab
7. Calculating the Probability:
- The probability P that the circular block falls entirely on one rectangular block is given by the ratio of the area of the smaller rectangle to the area of the original rectangle:
P=AreasmallArealarge=(a−c)(b−c)ab
8. Conclusion:
- Thus, the probability that the circular block falls entirely on one rectangular block is:
P=(a−c)(b−c)ab
- We have a rectangular block of dimensions a and b.
- A circular block of diameter c is thrown randomly onto the floor.
- We need to ensure that the entire circular block falls within the rectangular block.
- The radius R of the circular block is given by:
R=c2
- For the circular block to fall entirely on the rectangular block, the center of the circular block must be at least R (which is c2) away from the edges of the rectangular block.
- This means that the center of the circle must fall within a smaller rectangle formed inside the original rectangle.
- The effective length of the smaller rectangle where the center of the circle can fall is:
a−c
- The effective breadth of the smaller rectangle is:
b−c
- The area of the smaller rectangle where the center of the circle can fall is:
Areasmall=(a−c)(b−c)
- The area of the original rectangular block is:
Arealarge=ab
- The probability P that the circular block falls entirely on one rectangular block is given by the ratio of the area of the smaller rectangle to the area of the original rectangle:
P=AreasmallArealarge=(a−c)(b−c)ab
- Thus, the probability that the circular block falls entirely on one rectangular block is:
P=(a−c)(b−c)ab
Topper's Solved these Questions
Similar Questions
The area of a circular field is equal to the area of a rectangular field. The ratio of the length and the breadth of the rectangular field is 14:11 respectively and perimeter is 100 metres. What is the diameter of the circular field? (a) 14 m (b) 22 m (c) 24 m (d) 28 m (d) None of these
View SolutionThe floor of a rectangular hall is 24 m long and 18 m wide .How many carpets , each of length 2.5 m and breadth 80 cm , will be required to cover the floor of the hall ?
View Solution
Knowledge Check
The whole surface area of a rectangular block is 8788 sq cm. If length, breadth and height are in the ratio of 4 : 3:2, then find the length.
A26 cmB52 cmC104 cmD13 cmA rectangular block has length 10 cm, breadth 8 cm and height 2 cm. From this block , a cubical hole of side 2 cm is drilled out . Find the volume and the surface area of the remaining solid :
A152cm3,512cm2B125cm3,215cm2C152cm3,240cm2D125cm3,512cm2A rectangular wooden block has length 1.4 m and width 84 cm. What is the area of wooden block in appropriate significant figure?
A2.75 cmB3.75 cmC1.2m2D1.12m2 .
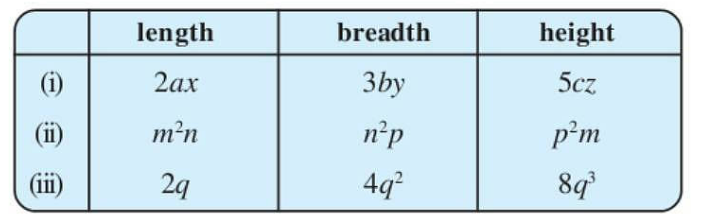
Find the volume of each rectangular box with given length, breadth and height.
View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionThe length of a rectangular plot is thrice its breadth. If the area of the rectangular plot is 7803 sq. metres, What is the breadth of the rectangular plot? (a) 51m (b) 88m (c) 104m (d) 153m (e) None of these
View SolutionA rectangular wooden block has length 1.4 m and width 84 cm. What is the area of wooden block in appropriate significant figure?
View SolutionThe total number of spherical bullets, each of diameter 5 decimeter, that can be made by utilizing the maximum of rectangular block of lead with 11 metre length, 10 metre breadth and 5 metre width is (assume that π>3)
View Solution
