Expand the following function in positive integral powers of the variable x up to the terms of the inficated order , inclusive
In cos x up to the terms containing x6
To expand the function cosx in positive integral powers of x up to the terms containing x6, we can use the Taylor series expansion of cosx around x=0.
The Taylor series expansion for cosx is given by:
cosx=∞∑n=0(−1)nx2n(2n)!
This means that the series consists of even powers of x with alternating signs. We will expand this series up to the term containing x6.
Step 1: Write down the terms of the series up to x6
The first few terms of the series are:
- For n=0:
(−1)0x2⋅0(2⋅0)!=x01=1
- For n=1:
(−1)1x2⋅1(2⋅1)!=−x22!=−x22
- For n=2:
(−1)2x2⋅2(2⋅2)!=x44!=x424
- For n=3:
(−1)3x2⋅3(2⋅3)!=−x66!=−x6720
Step 2: Combine the terms
Now, we combine all these terms to get the expansion of cosx up to x6:
cosx≈1−x22+x424−x6720
Final Result
Thus, the expansion of cosx in positive integral powers of x up to the terms containing x6 is:
cosx≈1−x22+x424−x6720
(−1)0x2⋅0(2⋅0)!=x01=1
(−1)1x2⋅1(2⋅1)!=−x22!=−x22
(−1)2x2⋅2(2⋅2)!=x44!=x424
(−1)3x2⋅3(2⋅3)!=−x66!=−x6720
Topper's Solved these Questions
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - TESTING A FUNCTION FOR MONOTONICITY
19 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - MAXIMA AND MINIMA OF FUNCTION
13 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - TAYLOR.S FORMULA .APPLICATION TO APPROXIMATE CALCULATIONS
5 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity
15 Videos
Similar Questions
Expand the following function in positive integral powers of the variable x up to the terms of the inficated order , inclusive
f(x)=e2x−x2 up to the terms containing x5
View SolutionIntegrate the following functions x2.sinx
View SolutionExpand the following expression using binomial theorem and write down their general term.
(x+2x)4
View SolutionIntegrate the following : sinxsin(cosx)
View SolutionIntegrate the following functions wrt respective variable: (1) sin2x (2) cos2x
View SolutionIf (x)=x2+λx+μ be an integral function of the integral variable x then
View SolutionWhat is the function of X in the given experimental set-up?
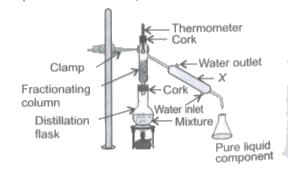
View SolutionIf (2+x3)55 is expanded in the ascending powers of x and the coefficients of powers of x in two consecutive terms of the expansion are equal then these terms are (A) 7,8 (B) 8,9 (C) 27,28 (D) 28,29
View SolutionFind the integrals of the functions cos2xcos4xcos6x
View SolutionIn the expansion of (1+x+7x)11find the term not containing x.
View Solution
