Prove the following inequalities :
tanx>x+x3/3if (0<x<π/2)
To prove the inequality tanx>x+x33 for 0<x<π2, we can define a function g(x) as follows:
g(x)=tanx−(x+x33)
We need to show that g(x)>0 for 0<x<π2.
Step 1: Differentiate g(x)
To analyze the behavior of g(x), we will differentiate it:
g′(x)=ddx(tanx)−ddx(x+x33)
Calculating the derivatives, we have:
g′(x)=sec2x−(1+x2)
Step 2: Simplify g′(x)
Now, we simplify g′(x):
g′(x)=sec2x−1−x2
Using the identity sec2x=1+tan2x, we can rewrite g′(x):
g′(x)=tan2x−x2
Step 3: Analyze g′(x)
We need to determine the sign of g′(x):
1. For 0<x<π2, tanx>0.
2. Since tanx increases faster than x as x approaches π2, tan2x>x2 in this interval.
Thus, g′(x)>0 for 0<x<π2, which means g(x) is an increasing function in this interval.
Step 4: Evaluate g(x) at the endpoints
Now, we evaluate g(x) at x=0:
g(0)=tan(0)−(0+033)=0−0=0
Since g(x) is increasing and g(0)=0, it follows that g(x)>0 for 0<x<π2.
Conclusion
Thus, we have shown that:
tanx>x+x33for 0<x<π2
2. Since tanx increases faster than x as x approaches π2, tan2x>x2 in this interval.
Topper's Solved these Questions
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - MAXIMA AND MINIMA OF FUNCTION
13 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - FINDING THE GREATEST AND THE LEAST VALUES OF A FUNCTION
11 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - APPLICATION OF TAYLOR.S FORMULA TO EVALUATION OF LIMITS
6 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity
15 Videos
Similar Questions
Knowledge Check
The solution of the following of inequalities 2x−3<7and 2x>−4 is
A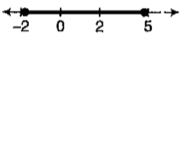 B
B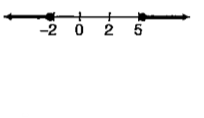 C
C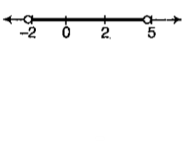 DNone of these
DNone of these
Solve the following equations :
2tan−1(sinx)=tan−1(2secx,)0<x<π2
View SolutionSolve the inequality: tanx<2
View SolutionProve the inequalities
x−x2<In(1+x)atx>0
View SolutionProve that tanx>x+x33 for all x∈(0,π2).
View SolutionProve the inequalities
1+12x−x28<√1+x<1+12x at 0<x<∞
View SolutionSolve the inequation : 0<x3<1
View SolutionSolve the following inequations:
(i) 3x−6<0
(ii) −3x+9≤0
(iii) 7x+5>33
(iv) 5x−15≥0.
View Solution
