The bob A of pendulum of length 1 m released from to the vertical hits another bob B of same mass at rest on the table. How high does the bob A rise after the collision and find the velocity of B.
The bob of pendulum acquires a velocity
,
on reaching the lower most position and makes elastic collision with the bob B of same mass.
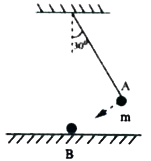
Hence the bodies simply exchange their velocities after collision. The bob of pendulum does not rise at all and velocity of B is
Topper's Solved these Questions
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 1A
117 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 1B
39 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
36 Videos
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - PRACTICE EXERCISE (PERFECTLY INELASTIC COLLISIONS)
5 Videos
Similar Questions
The bob A of a simple pendulum released from 30∘ to the vertical hits another bobo B of the same mass at rest on a table as shown in figure. How high does the bob A rise after the collision ? Neglect the size of the bobs and assume the collision to be elastic.
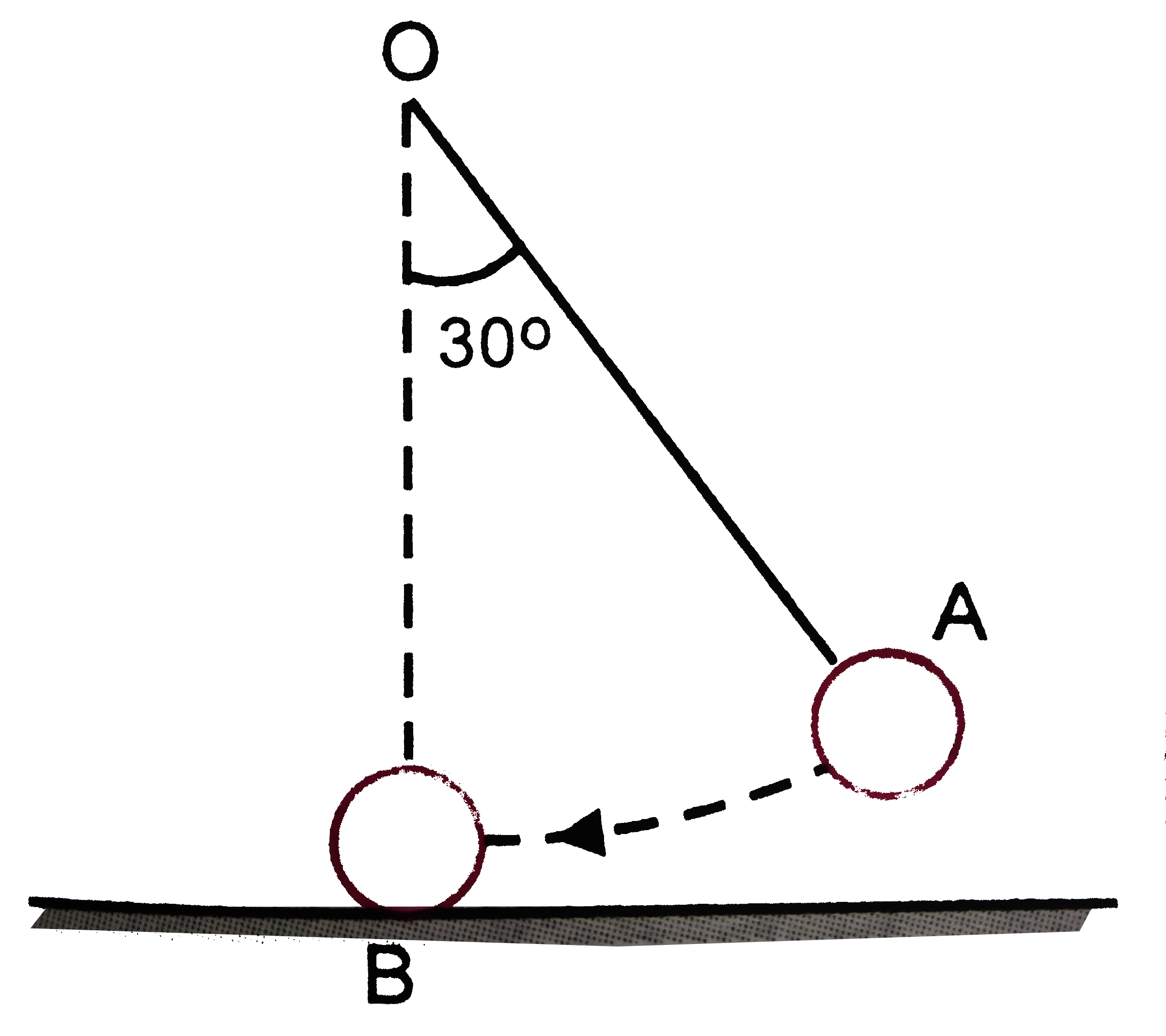
View SolutionThe bob A of a simple pendulum released from 30∘ to the vertical hits another bobo B of the same mass at rest on a table as shown in figure. How high does the bob A rise after the collision ? Neglect the size of the bobs and assume the collision to be elastic.

View Solution
Knowledge Check
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
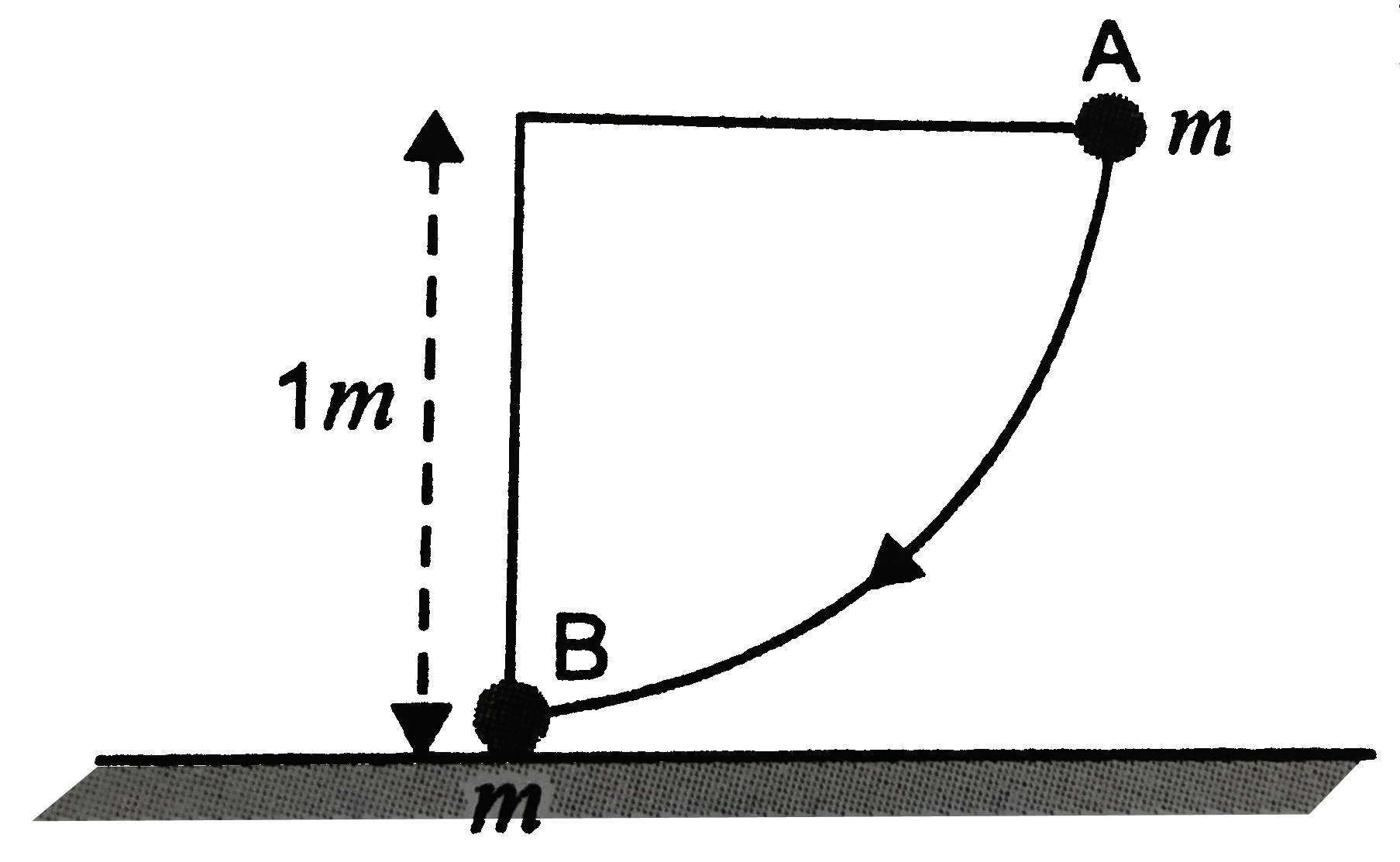 A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1
A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1The bob A of a simple pendulum is released when the string makes an angle of 45∘ with the vertical. It hits another bob B of the same meterial and same mass kept at rest on the table. If the collision is elastic, then
 ABoth AandB rise to the same heightBBoth AandB comes to rest at BCBoth AandB move with the same velocity of ADA comes to rest and B move with the same velocity of A
ABoth AandB rise to the same heightBBoth AandB comes to rest at BCBoth AandB move with the same velocity of ADA comes to rest and B move with the same velocity of AA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
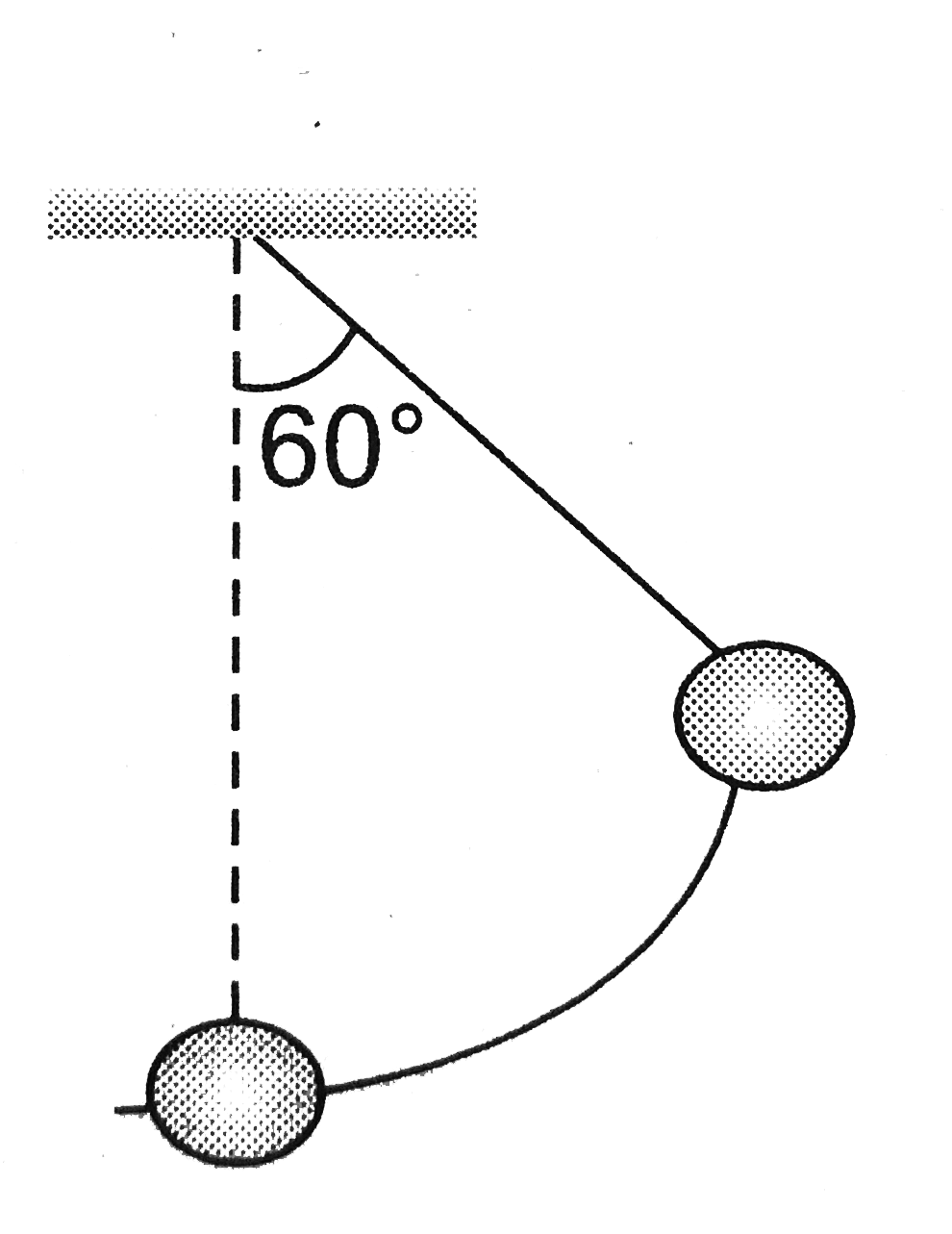 A5√3m/s2B5m/s2C10m/s2D2.5m/s2
A5√3m/s2B5m/s2C10m/s2D2.5m/s2
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.

View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.

View SolutionThe bob A of a simple pendulum is released when the string makes an angle of 45∘ with the vertical. It hits another bob B of the same material and same mass kept at rest on the table. If the collision is elastic, then

View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.

View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.

View Solution
