Two particles of masses 10 kg and 30 kg are lying on a straight line. The 10 kg mass is shifted towards the 30 kg mass by a distance of 2cm. By what distance should the 30kg mass be shifted so that the position of their centre of mass does not change Solution in Telugu
mass of the first block, m1=10kg
mass of the second block, m2=30kg
Let x1 and x.1 are positions of m1
x1 and x.1 are positions of m2
initially and later respectively
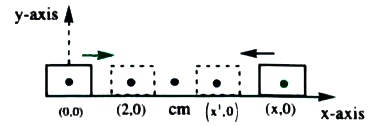
In this case of .xcm. is the position of centre of centre of mass then xcm=m1x1+m2+x2m1+m2
then the new position of CM when blocks are shifted x.cm=m1x.1+m2x.2m1+m2
subtracting the above equations
x.cm−xcm=m1(x1.−x1)+m2(x.2−x2)m1+m2
Δxcm=m1Δx1+m2Δx2m1+m2
0=10×2+30Δx240 ∴Δx2=−2/3
Therefore the second block should be moved left through a distance of 2/3 cm to keep the position of centre of mass unchanged.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE - 1A
120 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE - 1B
51 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
Similar Questions
Three identical spheres each of radius R are placed touching each other on a horizontal table. The centre of mass of the system is located
View Solution(A) : Position of centre of mass of a body (w.r.t body frame) is independent of co-ordinate system.
(R ) : Internal forces do not effect the motion of centre of mass.
View SolutionIf the work done in blowing a soap bubble of volume 'V' is W, then the work done in blowing a soap bubble of volume '2V' is
View SolutionA constant pressure gas thermometer has a volume of 200cc, 273.2cc and 525 .1cc at 0°C, 100°C and boiling point of sulphur respectively. The resistance possessed by a platinum wire at the same temperatures as above are 2.000Ω,2.778Ωand5.280Ω respectively. Estimate the boiling point of sulphur on the basis of the two sets of observations.
View SolutionCentre of mass of 3 particles 10 kg, 20 kg and 30 kg is at (0, 0, 0). Where should a particle of mass 40 kg be placed so that the combination centre of mass will be at (3,3,3)
View SolutionTwo particles of mass 2 kg and 4 kg lie on the same line. If 4 kg is displaced rightwards by 5m then by what distance 2 kg should be move for which centre of mass will remain at the same position
View SolutionTwo particles of masses 10 kg and 30 kg are lying on a straight line. The 10 kg mass is shifted towards the 30 kg mass by a distance of 2cm. By what distance should the 30kg mass be shifted so that the position of their centre of mass does not change
View SolutionTwo particles of masses 10 kg and 30 kg are lying on a stright line. The 10 kg mass is shifted towards the 30 kg mass by a distance of 2cm. By what distance should the 30 kg mass be shifted so that the position of their centre of mass does not change
View SolutionThe centre of mass of three particles of masses 10 kg, 20 kg and 30 kg is on origin (0, 0, 0). Now where should one place a mass of 40 kg, so that centre of mass of system is equal to (3, 3, 3)?
View SolutionTwo blocks of masses 10 kg and 30 kg are placed on x - axis. The first mass is moved on the axis by a distance of 2 cm. By what distance should the second mass be moved to keep the position of centre of mass unchanged.
View SolutionIf the centre of mass of three particles of masses of 1 kg, 2 kg, 3 kg is at (2,2,2), then where should a fourth particle of mass 4 kg be placed so that the combined centre of mass may be at (0,0,0) ?
View SolutionTwo particles of masses 10kg and 30kg are lying on a straight line. The 10kg mass is shifted towards the 30kg mass by a distance of 2cm. By what distance should the 30kg mass be shifted so that the position of their centre of mass does not change ?
View SolutionTwo particles of masses 10kg and 30kg are lying on a straight line. The 10kg mass is shifted towards the 30kg mass by a distance of 2cm. By what distance should the 30kg mass be shifted so that the position of their centre of mass does not change
View SolutionIf the centre of mass of three particles of masses of 1 kg, 2 kg, 3 kg is at (2,2,2), then where should a fourth particle of mass 4 kg be placed so that the combined centre of mass may be at (0,0,0).
View SolutionCentre of mass of 3 particles 10 kg, 20 kg and 30 kg is at (0, 0, 0). Where should a particle of mass 40 kg be placed so that the combined centre of mass will be at (3, 3, 3)?
View SolutionConsider a system of two particles having masses 2kg and 5 kg the particle of mass 2 kg is pushed towards the centre of mass of particles through a distance 5 m,by what distance would particle of mass 5kg move so as to keep the centre of mass of particles at the original position?
View Solution
