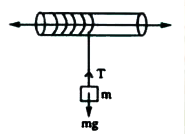
A solid cylinder of mass M and radius .R. is mounted on a frictionless horizontal axle so that it can freely rotate about this axis. A string of negligible mass is wrapped round the cylinder and a body of mass .m. is hung from the string. The mass is released from rest. Find the tension in the string and the angular speed of cylinder as the mass falls a distance h.
The acceleration .a. of the falling body is given by
mg−T=ma ……(1)
Torque on the cylinder is τ=TR=Iα
∴T=IαR=(MR22)(aR2) [∵α=aR]
or T=Ma2 .....(2)
from (1) and (2) T=mMg(M+2m)
from consevation of energy,
we have mgh=12mv2+12Iω2
=12m(Rω)2+12(MR22).ω2
on solving ω=[4mgh(M+2m)R2]12
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE - 1A120videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE - 1B51videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )8videos
SURFACE TENSION
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions2videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.
 View Solution
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
AmgM+mB2mgM+mC2mgM+2mD2mg2M+m - Question 2 - Select One
A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
A4mgM+2mB4mgM+4mC2mgM+mD2mgM+2m - Question 3 - Select One
A uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
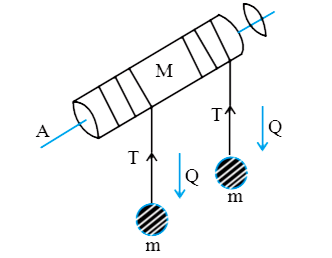 AMmgM+mBMmgM+2mCMmgM+3mDMmgM+4m
AMmgM+mBMmgM+2mCMmgM+3mDMmgM+4m
A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
 View Solution
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
 View Solution
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
 View Solution
View SolutionA uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
 View Solution
View Solution

