A force →F=3ˆj acts on the rod at a point P(1,0,0). Here centre of rod is taken as origin. Then the torque about .O. is
A
3ˆk
B
−ˆk
C
ˆk3
D
−ˆk3
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- VECTORSBOOK - AAKASH SERIESCHAPTER - VECTORSEXERCISE - Practice Sheet (Exercise-III) (Multiplication of Vectors (Level-II)) (Linked Comprehension Type Questions)
2 Videos
- VECTORSBOOK - AAKASH SERIESCHAPTER - VECTORSEXERCISE - Additional Practice Exercise (Level-I(Main)) (Straight Objective Type Questions)
10 Videos
- VECTORSBOOK - AAKASH SERIESCHAPTER - VECTORSEXERCISE - Practice Sheet (Exercise-III) (Multiplication of Vectors (Level-I)) (Straight Objective Type Questions)
35 Videos
- UNITS AND MEASUREMENTS BOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTS EXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
14 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
Similar Questions
Knowledge Check
A force →F=3ˆi+2ˆj−4ˆk is applied at the point (1,−1,2). What is the moment of the force about the point (2,−1,3)?
Aˆi+4ˆj+4ˆkB2ˆi+ˆj+2ˆkC2ˆi−7ˆj−2ˆkD2ˆi+4ˆj+ˆkA force F=2ˆi+3ˆj−ˆk acts at a point (2,-3,1). Then magnitude of torque about point (0,0,2) will be
A6 unitsB3√5 unitsC6√5 unitsDNone of theseThe torque of a force →F=−2ˆi+2ˆj+3ˆk acting on a point →r=ˆi−2ˆj+ˆk about origin will be
A(17ˆj+5ˆk−3ˆi)NmB(2ˆj+4ˆj−6ˆk)NmC(12ˆi−5ˆj+7ˆk)NmD(−13ˆj+22ˆi+ˆk)Nm
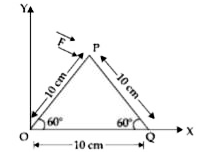
A triangular plate is shown. A force →F=4ˆi−3ˆj is applied at point P. The torque at point P with respect to point 'O' and 'Q ' are :
View SolutionTwo forces →F1=2ˆi−5ˆj−6ˆkand→F2=−ˆi+2ˆj−ˆk are acting on a body at the points (1, 1, 0) and (0, 1, 2) . Find torque acting on the body about point (- 1, 0, 1)
View SolutionA force →F=(2ˆi+3ˆj−5ˆk)N acts at a point →r1=(2ˆi+4ˆj+7ˆk)m. The torque of the force about the point →r2=(ˆi+2ˆj+3ˆk)m is
View SolutionA force →F=3ˆi+2ˆj−4ˆk is applied at the point (1,−1,2). Find the moment of →F about the point (2,−1,3).
View SolutionFind the torque of a force →F=(2ˆi+ˆj−3ˆk)N about a point O. The position vector of point of application of force about O is →r=(2ˆi+3ˆj−ˆk)m.
View Solution
