A projectile of mass m, charge Z., initial speed v and impact parameter b is scattered by a heavy nucleus of charge Z. Use angular momentum and energy conservation to obtain a formula connecting the minimum distance (s) of the projectile form the nucleus to these parameters. Show that for b = 0, s reduces to the closest distance of approach $r_{0}$ .

Text Solution

Verified by Experts

Fig. shows the conditions of the problem.
Charge on the nucleus = Ze
Charge on the projectile = Z.e

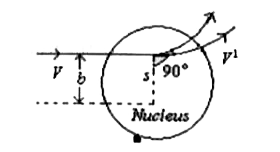
At infinity, the angular momentum of projectile about the nucleus = mvb
When the projectile is at the minimum distance s from the nucleus, its velocity vector v. is normal to the radius vector (drawn from the centre of the nucleus).
$∴$ Angular momentum of the projectile about the nucleus = mv.s
From the law of conservation of angular momentum, we have,
mvb = mv.s or $v . = \frac{v b}{s}_{_}__{_}__{i}$
When the projectile is infinitely away from the nucleus, it has only kinetic energy ( $∵$ P.E = 0) given by,
$E_{k} = \frac{1}{2} m v^{2}$
When the projectile is at minimum distance s from the nucleus, it has both kinetic and potential energies given by,
$E_{k} = \frac{1}{2} m v .^{2}$ and $E ._{p} = \frac{1}{4 π ε_{0}} . \frac{ZZ . e^{2}}{s}$
From the law of conservation of energy, we have,
$E_{k} + E_{p} = E_{k}$
or $\frac{1}{2} m v .^{2} + \frac{1}{4 π ε_{0}} . \frac{ZZ . e^{2}}{s} = \frac{1}{2} m v^{2}$
Putting v. = vb/s from eq. (i), we get,
$\frac{1}{2} m \frac{v^{2} b^{2}}{s^{2}} + \frac{1}{4 π ε_{0}} . \frac{ZZ . e^{2}}{s} = \frac{1}{2} m v^{2}$
Dividing both sides by $m v^{2} / 2$ , we get,
$\frac{b^{2}}{s^{2}} + \frac{1}{4 π ε_{0}} . \frac{ZZ . e^{2}}{s (m v^{2} / 2)} = 1$ or $s^{2} = b^{2} + \frac{1}{4 π ε_{0}} . \frac{ZZ . e^{2} s}{m v^{2} / 2}$
This is the required formula.
For a head-on collision, b = 0.
$∴ s^{2} = \frac{1}{4 π ε_{0}} . \frac{ZZ . e^{2} s}{m v^{2} / 2} ∴ s = \frac{1}{4 π ε_{0}} . \frac{ZZ . e^{2} s}{m v^{2} / 2}$
which is the distance of closest approach

Updated on:21/07/2023