Find $V_{a b}$ in an electric field $\to E = (2 ˆ i + 3 ˆ j + 4 ˆ K) N / C$ where ${\to i}_{a} = (ˆ i - 2 ˆ j + ˆ k) m and \to r_{b} = (2 ˆ i + ˆ j - 2 ˆ k) m$ Solution in Telugu

2 volt

$- 1$ volt

1 volt

3 volt

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Find V_(ab) in an electric field vec(E)=(2hat(i)+3hat(j)+4hat(K))N//C where vec(i)_(a)=(hat(i)-2hat(j)+hat(k))mandvec(r_(b))=(2hat(i)+hat(j)-2hat(k))m by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
6 Videos
ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
4 Videos
ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - III) (LEVEL - II (ADVANCED) INTEGER TYPE QUESTIONS)
2 Videos
ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos

Similar Questions

Two metallic solid spheres of radii R and 2R are changed such that both of them have same charge density $σ$ . If the spheres are located for away from each other and connected by a conducting wire, the new charge density on bigger sphere is :
View Solution
Four charges of 1 mC, 2mC, 3mC and- 6 mC are placed one at each corner of the square of side 1m. The square lies in the x-y plane with its centre at the origin.
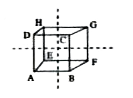
View Solution
Two infinite line charges, each having a uniform density $λ$ . Pass through the midpoints of two pairs of opposite faces of a cube of edge L as shown in figure. The modulus of the total electric flux due to both the line charges through the face is ABCD is $λ L / (k ε_{0})$ find the value of k ?

View Solution
What is the radius of the path of an electron (mass 9 × 10-31 kg and charge $1.6 \times x 10^{- 19}$ C) moving at a speed of $3 \times x 10^{7}$ m/s in a magnetic field of $6 x \times 10^{- 4}$ T perpendicular to it? What is its frequency? Calculate its energy in keV. $(1 e V = 1.6 \times 10^{- 19} J)$
View Solution
Find the components of vector $¯ ¯ ¯ A = 2 ˆ i + 3 ˆ j$ along the directions of $ˆ i + ˆ j and ˆ i - ˆ j$
View Solution
Find the projection of $\to b + \to c$ on $\to a$ , where $\to a$ = $2 ˆ i - 2 ˆ j + ˆ k, = ˆ i + 2 ˆ j - 2 ˆ j - 2 ˆ k$ and $\to c = 2 ˆ i - ˆ j + 4 ˆ k$ .
View Solution
If vec a=4hat i+3hat j+hat k and vec b=hat i-2hat k, then find |2hat bxvec a|
View Solution
$\to a = 2 ˆ i - ˆ j + ˆ k, \to b = ˆ i + 2 ˆ j - ˆ k, \to c = ˆ i + ˆ j - 2 ˆ k .$ A vector coplanar with $\to b a n d \to c$ whose projectin on $\to a$ is magnitude $\sqrt{\frac{2}{3}}$ is $2 ˆ i + 3 ˆ j - 3 ˆ k$ b. $- 2 ˆ i - ˆ j + 5 ˆ k$ c. $2 ˆ i + 3 ˆ j + 3 ˆ k$ d. $2 ˆ i + ˆ j + 5 ˆ k$
View Solution
vec r=(4hat i-hat j)+lambda(hat i+2hat j-3hat k) and vec r=(hat i-hat j+2hat k)+mu(2hat i+4hat j-5hat k)
View Solution
If vec a=2hat i+2hat j+3hat k,vec b=-hat i+2hat j+hat k and vec c=3hat i+hat j then vec a+tvec b is perpendicular to vec c if t=
View Solution
If vec a=3hat i-2hat j+4hat k and vec b=hat i-hat j+2hat k then find the modulus of vec a-vec b
View Solution
If vec a=2hat i+hat j+hat k,vec b=3hat i-4hat j+2hat k and vec c=hat i-2hat j+2hat k then the projection of vec a+vec b is
View Solution
If $\to A = 3 ˆ i + ˆ j + 2 ˆ k$ and $\to B = 2 ˆ i - 2 ˆ j + 4 ˆ k,$ then find the value of $∣ ∣ \to A \times \to B ∣ ∣ .$
View Solution
vec(A)=hat(j)-2hat(i)+3hat(k) " , "vec(B)= hat(i)+2hat(j)+2hat(k) find vec(A).vec(B)
View Solution
Find $[\to a \to b \to c]$ , when
$(i) \to a = 2 ˆ i + ˆ j + 3 ˆ k, \to b = - ˆ i + 2 ˆ j + ˆ k and \to c = 3 ˆ i + ˆ j + 2 ˆ k$
(ii) $\to a = 2 ˆ i - 3 ˆ j + 4 ˆ k, \to b = ˆ i + 2 ˆ j - ˆ k and \to c = 3 ˆ i - ˆ j + 2 ˆ k$
(iii) $\to a = 2 ˆ i - 3 ˆ j, \to b = ˆ i + ˆ j - ˆ k and \to c = 3 ˆ i - ˆ k$
View Solution
Show that the vectors $\to a, \to b, \to c$ are coplanar, when
(i) $\to a = ˆ i - 2 ˆ j + 3 ˆ k, \to b = - 2 ˆ i + 3 ˆ j - 4 ˆ k and \to c = ˆ i - 3 ˆ j + 5 ˆ k$
(ii) $\to a = ˆ i + 3 ˆ j + ˆ k, \to b = 2 ˆ i - ˆ j - ˆ k and \to c = 7 ˆ j + 3 ˆ k$
(iii) $\to a = 2 ˆ i - ˆ j + 2 ˆ k, \to b = ˆ i + 2 ˆ j - 3 ˆ k and \to c = 3 ˆ i - 4 ˆ j + 7 ˆ k$
View Solution

AAKASH SERIES-ELECTROSTATICS-LECTURE SHEET (EXERCISE - IV) (LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)

If the electri potential of the inner metal sphere is 10 volt & that ...
02:03
A uniform electric field of 100 V/m is directed at 30^(@) with the pos...
05:58
Find the potential function V (x,y) of an electrostatic field vec(E)=2...
08:03
A solid metall sphere of radius R has a charge + 2Q. A hollow spherica...
05:31
Two equal positive charges are kept at points A and B. The electric po...
Text Solution
Find V(ab) in an electric field vec(E)=(2hat(i)+3hat(j)+4hat(K))N//C w...
05:33
For a sphericla shell
Text Solution
There are two concentric spherical shells of ratii r and 2r. Intially ...
Text Solution
Figure shows three circular ars, each of radis R and total charge as i...
Text Solution
An infinite nonconducting sheet of charge has a surface charge density...
04:28

Home
Ask Doubt
Profile

Find Vab in an electric field →E=(2ˆi+3ˆj+4ˆK)N/C where →ia=(ˆi−2ˆj+ˆk)mand→rb=(2ˆi+ˆj−2ˆk)m Solution in Telugu

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

AAKASH SERIES-ELECTROSTATICS-LECTURE SHEET (EXERCISE - IV) (LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)

Find $V_{a b}$ in an electric field $\to E = (2 ˆ i + 3 ˆ j + 4 ˆ K) N / C$ where ${\to i}_{a} = (ˆ i - 2 ˆ j + ˆ k) m and \to r_{b} = (2 ˆ i + ˆ j - 2 ˆ k) m$ Solution in Telugu