The electric field in a region of space varies as E=(3v/m)xˆi+(4v/m)yˆj+(5v/m)zˆk Consider a differential cube whose one vertex is (x, y, z) and the three sides are dx, dy, dz, sides being parallel to the three coordinate axes.
The flux of electric field through the differential cube is zero
The flux of electric field through the cube = 12 dx dy dz
The charge enclosed by the cube is zero.
The charge enclosed by a spherical surface of radius r, centered at origin is 16πε0r3
The correct Answer is:B, D
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)3videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) MATRIX MATCHING TYPE QUESTIONS1videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTION)14videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE6videos
ELECTROMAGNETICS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS9videos
ELEMENTS OF VECTORS
Similar Questions
The electric field in a region of space varies as E=(xˆi+2yˆj)+3zˆk) V/m
(a). Consider an elemental cuboid whose one vertex is at (x,y,z) and the three sides are dx, dy and dz, sides being parallel to the three co-ordinate axes. Calculate the flux of electric field through the cube.
(b). Usig the expression obtained in (a) find the charge enclosed by a spherical surface of radius r, centred at the origin.View SolutionThe electric field in a region is given as
E=1ε0[(2y2+z)ˆi+4xyˆj+xˆk]V/m
Find volume charge density at ( - 1, 0,3) .View Solution
Knowledge Check
- Question 1 - Select One
The electric field in a certain region is given by E=5ˆi−3ˆjkv/m. The potential difference VB−VA between points a and B having coordinates (4, 0, 3) m and (10, 3, 0) m respectively, is equal to
A21 kVB−21kVC39kVD−39kV - Question 2 - Select One
In a region of space the electric field in the x-direction and proportional to xi.e., →E=E0xˆi. Consider an imaginary cubical volume of edge a with its sides parallel to the axes of coordinates. The charge inside this volume will be
AzeroBε0E0a3C1ε0E0a3D16ε0E0a3
The electric field ina region is given as
E=1ε0[(2y2+z)ˆi+4xyˆj+xˆk]V/m
Find volume charge density at ( - 1, 0,3) .View SolutionElectric field in a region is given by →E=−4xˆi+6yˆj. Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram
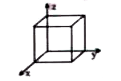 View Solution
View SolutionThe electric field in a certain region is given by E=5ˆi−3ˆjkv/m. The potential difference VB−VA between points a and B having coordinates (4, 0, 3) m and (10, 3, 0) m respectively, is equal to
View SolutionThe electric field in a region of space is given as ¯¯¯E=(5xˆi−2ˆj) .Potential at point x=1 y=1 is V1 and potential at point (x=2 y=3) is V2 .Then V1−V2 is equal to
View SolutionThe electric field in a region of space is given as ¯¯¯E=(5xˆi−2ˆj) .Potential at point x =1 y=1 is V1 and potential at point x =2 y=3 is V2 .ThenV1−V2 is equal to
View SolutionThe electric field in a region of space has the components Ey=Ez=0andEx=(4.00N/C)x2. Point A is on the y axis at y = 3.00 m, and point B is on the x axis at x = 4.00 m. What is the potential difference VB−VA ?
View Solution

