An infinitely long line charge having a uniform charge per unit length lies a distance d. From center of imaginary sphere of radius R. Then
Flux crossing the sphere is zero if d gt R b)
Flux crossing the sphere is , if
If , the magnitude of maximum potential difference two points on the sphere is
When a charge is moved along any dimeter of the sphere in the plane perpendicular to the wire, work done is zero.
The correct Answer is:A, B, C
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
2 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED)MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
20 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
Similar Questions
An infinitely long line charge having a uniform charge per unit length λ lies at a distance d from a point O as shown in figure. Determine the total electric flux through through the surface of a sphere of radius R centered at O resulting from this line charge. Consider both cases where Rltd and Rgtd.

View SolutionAn infinitely long line charge having a uniform charge per unit length λ lies at a distance d from a point O as shown in figure. Determine the total electric flux through through the surface of a sphere of radius R centered at O resulting from this line charge. Consider both cases where R<d and R>d.

View Solution
Knowledge Check
A uniformly charged and infinitely long line having a linear charge density 'λ' is placed at a normal distance y from a point O. Consider a sphere of radius R with O as centre and R>y. Electric flux through the surface of the sphere is
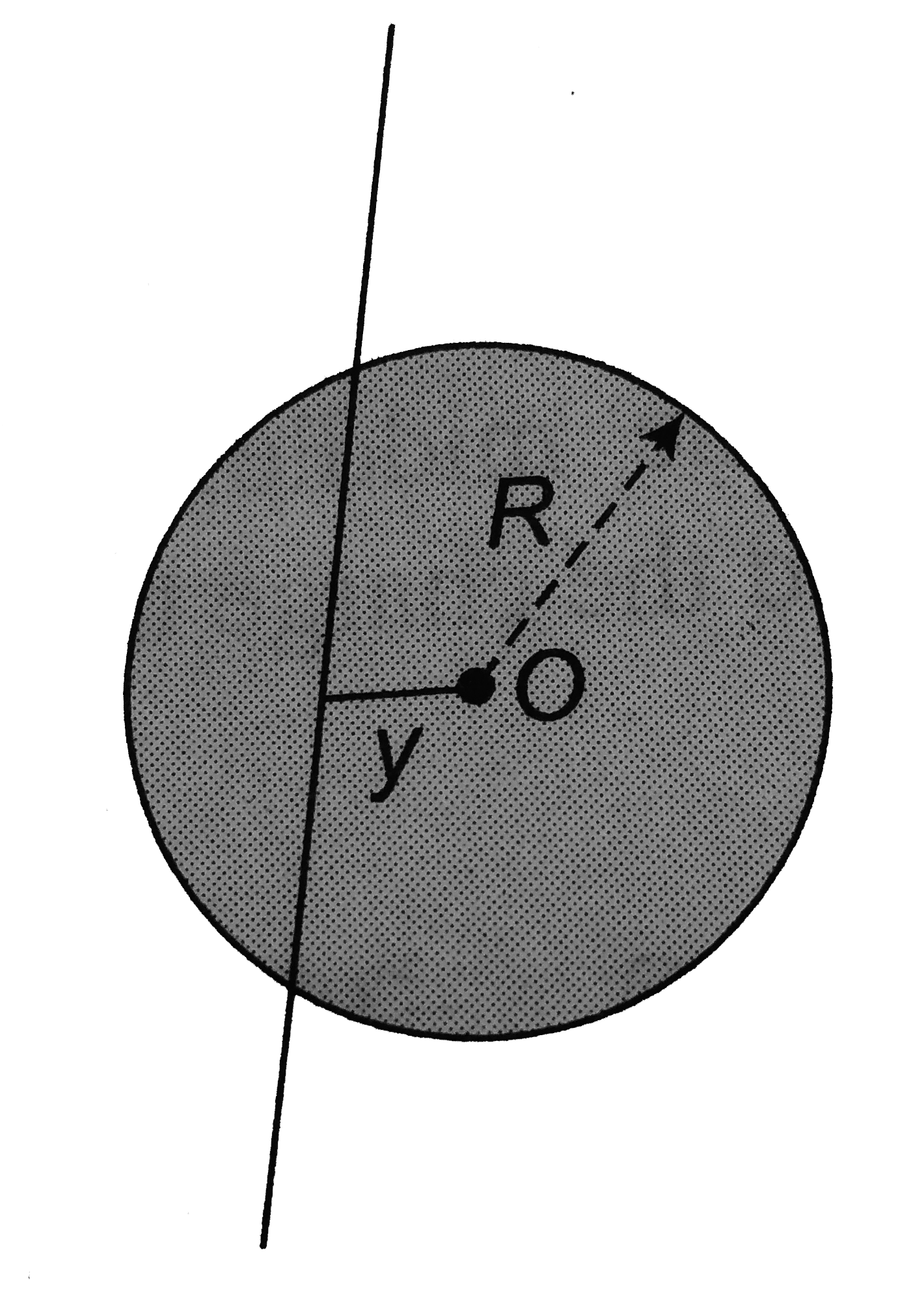 AzeroB2λRε0C2λ√R2−y2ε0Dλ√R2+y2ε0
AzeroB2λRε0C2λ√R2−y2ε0Dλ√R2+y2ε0The electric field at a distance r from a long wire having charge per unit length λ is
AE=2πε0λKr2BE=ε0λ2πKr2CE=λ2πε0KrDE=4πε0λKr2The electric field at a distance r from a long wire having charge per unit length λ is
Ak(λr2)Bk(λr)Ck(λ2r)Dk(2λr)
An infinitely long line charge having a uniform charge per unit length λ lies at a distance d from a point O as shown in figure. Determine the total electric flux through through the surface of a sphere of radius R centered at O resulting from this line charge. Consider both cases where R<d and R>d.

View SolutionA uniformly charged and infinitely long line having a linear charge density 'λ' is placed at a normal distance y from a point O. Consider a sphere of radius R with O as centre and R>y. Electric flux through the surface of the sphere is

View SolutionA uniformly charged and infinitely long line having a linear charge density 'λ' is placed at a normal distance y from a point O. Consider a sphere of radius R with O as centre and R>y. Electric flux through the surface of the sphere is

View SolutionThere is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
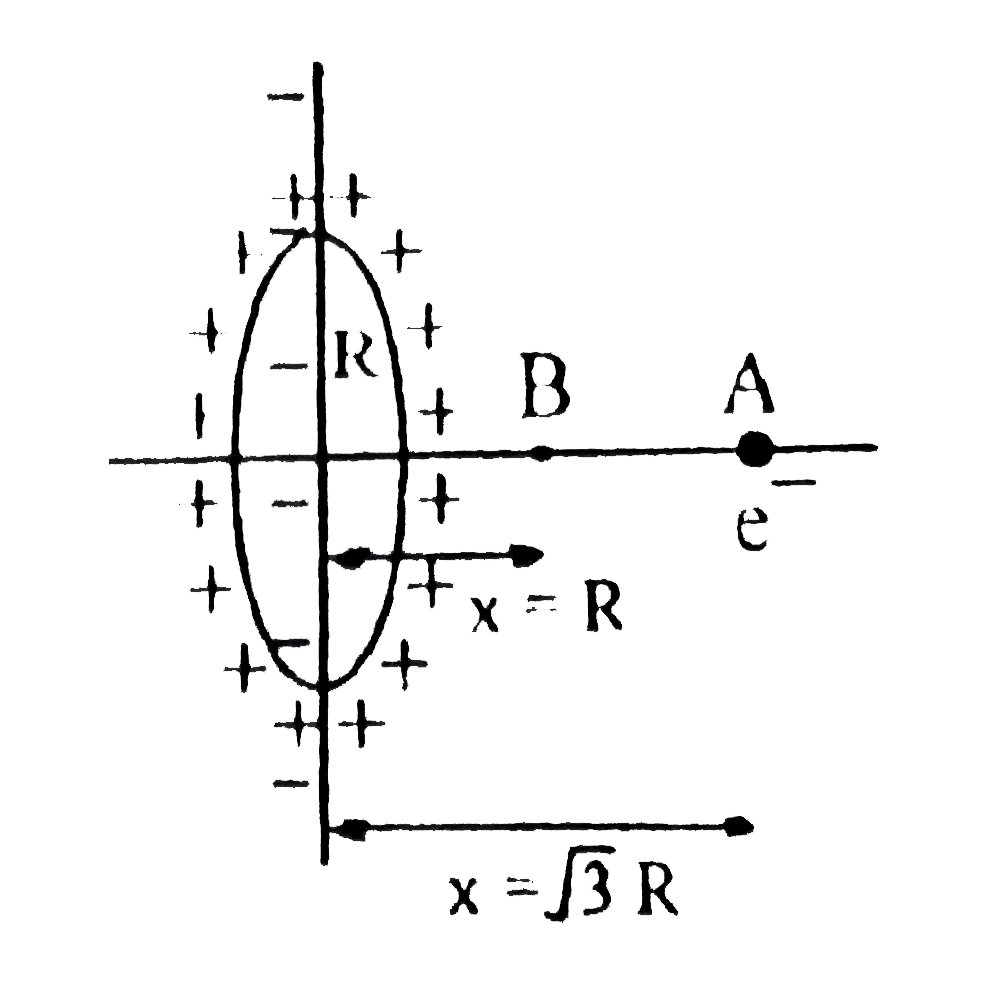
The distance from centre of ring on the axis where the net force on the electron is zero.
View SolutionThere is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
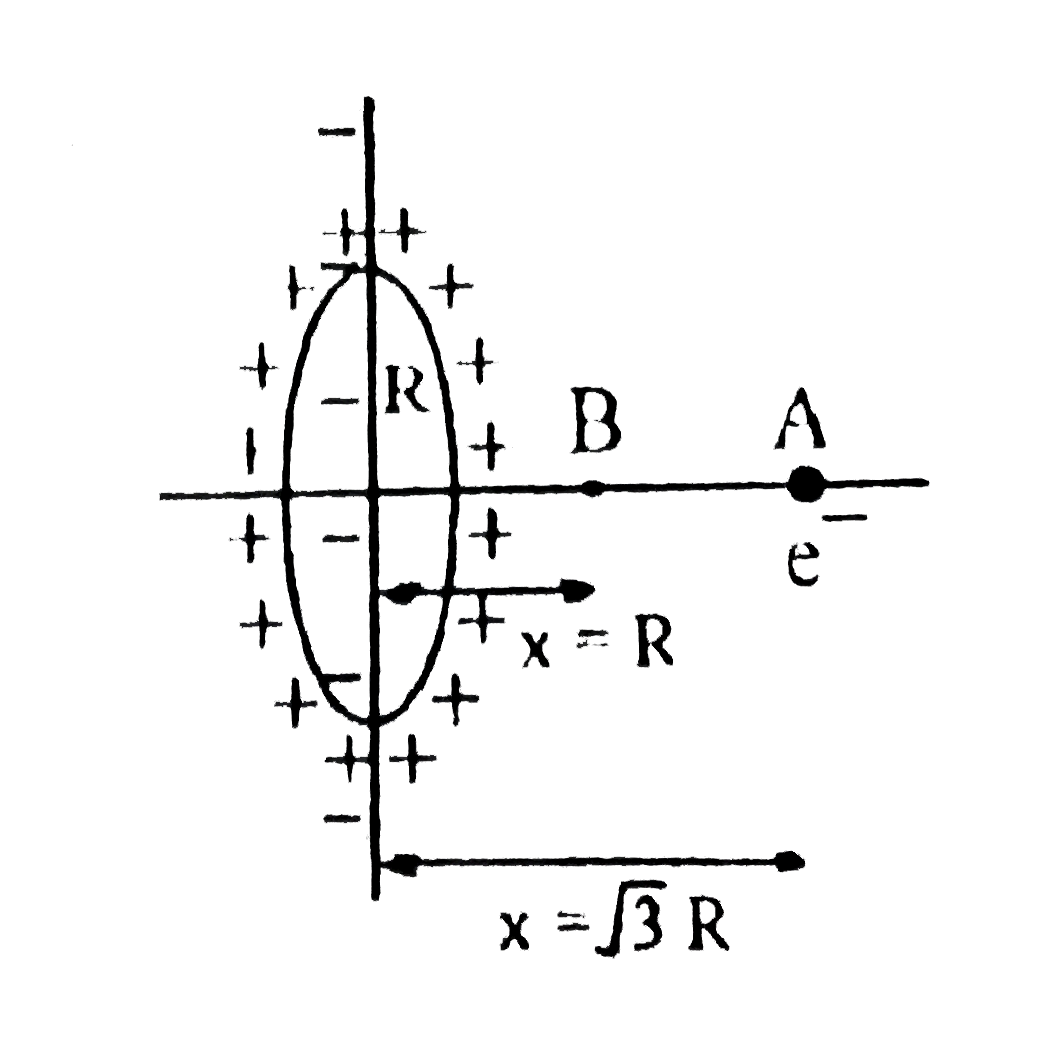
Potential difference between points A(x=√3R) and B(x=R)i.e.(VA−VB) is
View Solution
